Enunciado
Cálculo - Um curso de Cálculo Volume 2 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 3.5 - Ex. 2b
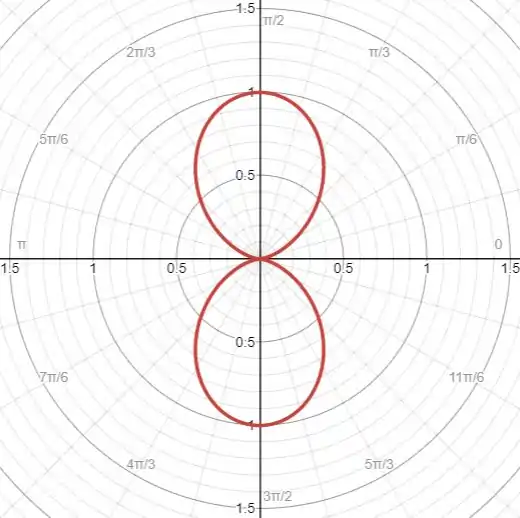
Passe a curva dada para coordenadas polares e desenhe-a.
Passo 1
Utilizando a substituição
Para transformar a equação para coordenadas polares
Passo 2
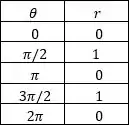
Montando a tabelinha de e , com os ângulos principais:
Passando os valores para o plano e esboçando a curva
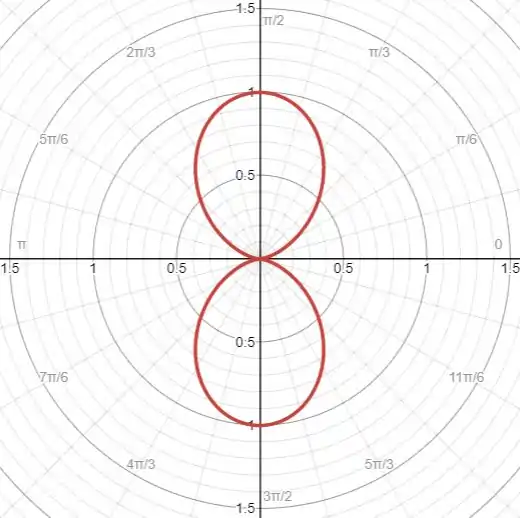
Resposta
Exercícios de Livros Relacionados
Encontre a área da região sombreada.
Encontre a área da região sombreada.
Calcule a integral, interpretando-a em termos das áreas. ∫ - 1 3 3 - 2 xd x
O gráfico de g consiste em duas retas e um semicírculo. Use-o para calcular cada integral.
Calcule a integral, interpretando-a em termos das áreas. ∫ - 2 2 4 - x 2d x