Enunciado
Cálculo - Um curso de Cálculo Volume 2 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 3.5 - Ex. 6
Calcule a área da região situada no quadrante, limitada acima pela curva (coordenadas cartesianas) e abaixo por (coordenadas polares), com .
Passo 1
Primeiramente vamos transformar em coordenadas polares, como foi feito na questão 2
E então desenhamos essa curva e a curva no plano polar e ficamos com
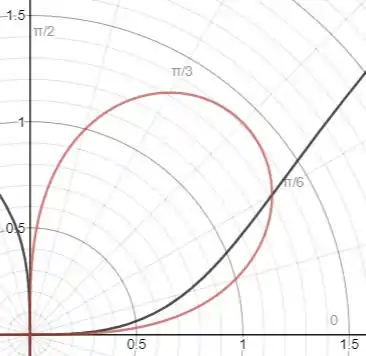
E temos que a área de uma curva polar e, um intervalo é dada por
E a área entre as duas curvas vai ser
Passo 2
Precisamos então encontrar o intervalo de integração, onde as funções se cruzam, para isso igualamos
Se temos e essa é uma solução válida, agora assumindo que
Temos as soluções e que são os nossos limites de integração.
Passo 3
A área então é dada por
Calculando as integrais separadamente, começando com a do seno
E a integral da tangente
Fazendo a substituição
Retornando a variável inicial
Portanto temos
Nos limites de integração