Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 6.1 - Ex. 32
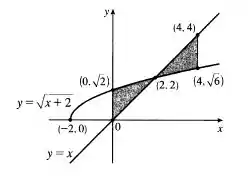
Calcule a integral e interprete-a como a área de uma região. Esboce a região.
Passo 1
Bom galera, nesse exercício iremos calcular a integral apresentada e interpretar como a área de uma região. Dessa forma, após calcular a integral iremos esboçar a região em questão.
Passo 2
Primeiro vamos simplificar a integral devido ao módulo da seguinte maneira:
Agora resolvemos cada integral:
Assim temos:
Passo 3
Aplicando os limites de integração, temos
Passo 4
Para o esboço do gráfico vamos dividir em duas curvas:
Agora é só desenhar:
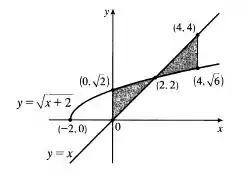
Lembra que a nossa integral estava em módulo, então todo o resultado que nos interessa é essa rachurada! O que faz bastante sentido pois o valor de uma área é sempre positivo!
Resposta
Exercícios de Livros Relacionados
Se A unidades quadradas for a área da região limitada pela parábola y 2 = 4 x e pela reta y = m x ( m0 ) , acha a taxa de variação de A em relação a m .
Determine m de tal forma que a região acima da curva y = m x 2 m0 , à direita do eixo y e abaixo da reta y = m tenha uma área de K unidades quadradas, onde K0 .
Use um gráfico para encontrar os valores aproximados das coordenadas x dos pontos de intersecção das curvas indicadas. A seguir, encontre a área aproximada da região delimitada pelas curvas. y = 3 x 2
Use um gráfico para encontrar os valores aproximados das coordenadas x dos pontos de intersecção das curvas indicadas. A seguir, encontre a área aproximada da região delimitada pelas curvas. y = 3 x 2
52. As taxas nas quais a chuva cai, em centímetros por hora, em dois locais diferentes, t horas após o começo da tempestade são dadas por f t = 0,73 t 3 - 2 t 2 + t + 0,6 e g t = 0,17 t 2 - 0,5 t + 1,