Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 5.3 - Ex. 54
Calcule a integral e interprete-a como uma diferença de áreas. Ilustre com um esboço.
54)
Passo 1
Primeiro vamos calcular a integral. Como temos uma função trigonométrica, o seu resultado é tabelado:
Agora é só substituir o x pelo intervalo dado:
Tranquilinho, não é?
Agora vamos esboçar o gráfico.
Passo 2
Esboçando o cosseno no intervalo de até
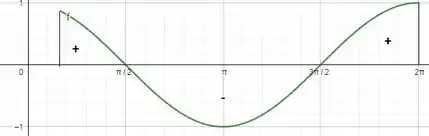
Então nós temos a área sendo representada por sinal positivo quando está acima do eixo x e negativa quando está abaixo. Como a área abaixo do gráfico é maior que a área acima o resultado da integral fornece resultado negativo!
Resposta
Exercícios de Livros Relacionados
Se f x for a inclinação de uma trilha a uma distância de x milhas do começo dela, o que ∫ 3 5 f x d x representa?
Se vazar óleo de um taque a uma taxa de r t galões por minuto em um instante t , o que ∫ 0 120 r t d t representa?
A corrente em um fio elétrico é definida como a derivada da carga: I t = Q ' t (veja o Exemplo 3 da Seção 3.7 ). O que ∫ a b I t d t representa?
Uma colmeia com uma população inicial de 100 abelhas cresce a uma taxa de n ' t abelhas por semana. O que 100 + ∫ 0 15 n ' t d t representa?
Na Seção 4.7 definimos a função rendimento marginal R ' x como a derivada da função rendimento R x , onde x é o número de unidades vendidas. O que ∫ 1000 5000 R ' x d x representa?