Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 15.4 - Ex. 31

Calcule a integral iterada, convertendo-a antes para coordenadas polares.

∫ 0 1 ∫ y 2 - y 2 ( x + y )   d x   d y

Passo 1

E aiii minha galerinha, tudo na paz com vocês?! Vamos nessa!

Nessa questão, precisamos calcular a integral iterada abaixo convertendo antes em coordenadas polares:

∫ 0 1 ∫ y 2 - y 2 ( x + y )   d x   d y

Antes te tudo, vamos lembrar como é escrito coordenadas polares. Temos um círculo de raio r :

x 2 + y 2 = r 2

Em coordenadas polares vamos ter:

x = r cos ⁡ θ

y = r   s e n   θ

d x d y = r d r d θ

Sabendo disso, nosso objetivo é avaliar nossa região de integração. Repare que:

y ≤ x ≤ 2 - y 2

Dessa informação, a gente consegue descobrir os intervalos de integração em coordenadas polares. Basta igualarmos assim:

y ≤ x

x ≤ 2 - y 2

E substituir os respectivos termos em coordenadas polares.

Feito isso, você volta para integral e deixa tudo em coordenadas polares. Depois e só resolver.

Bora lá fazer isso!

Passo 2

Vamos começar determinando nossos intervalos em coordenadas polares.

Galera, repare que o intervalo de integração em x é:

y ≤ x ≤ 2 - y 2

Disso, podemos concluir que:

x ≤ 2 - y 2

y ≤ x

Agora devemos avaliar cada caso. Mas lembre-se de substituir para coordenadas polares:

x = r cos ⁡ θ

y = r   s e n   θ

Vamos avaliar primeiro: x ≤ 2 - y 2

Em coordenadas polares temos:

r cos ⁡ θ ≤ 2 - r 2 s e n 2 θ

r 2 cos 2 ⁡ θ ≤ 2 - r 2 s e n 2 θ

r 2 ≤ 2

r ≤ ± 2

Então já sabemos que:

0 ≤ r ≤ 2

Vamos usar apenas a componente positiva do raio, porque não faz sentido termos um raio negativo.

Usando a outra inequação, temos:

y ≤ x

Em coordenadas polares:

r   s e n   θ ≤ r cos ⁡ θ

s e n   θ ≤ cos ⁡ θ

Qual o ângulo que o cosseno é igual ao seno? Vamos avaliar um círculo trigonométrico:

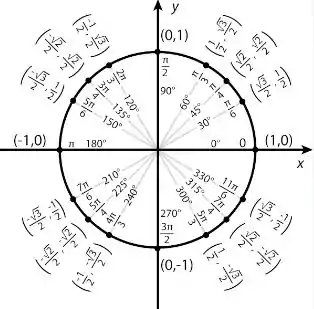
Repare que eles serão iguais em 45 ° e 225 ° graus.

Mas do intervalo de integração em y temos que:

0 ≤ y ≤ 1

Logo,

y ≥ 0

y ≤ 1

Repare que os valores de y são positivos, logo só podemos estar no primeiro quadrante.

Então restringiremos nossa região a:

0 ≤ θ ≤ π 4

Passo 3

Agora podemos começar a montar nossa integral em coordenadas polares.

A integral inicial era:

∫ 0 1 ∫ y 2 - y 2 ( x + y )   d x   d y

Os limites de integração já encontramos:

0 ≤ θ ≤ π 4

0 ≤ r ≤ 2

Sabemos também que:

x = r cos ⁡ θ

y = r   s e n   θ

d x d y = r d r d θ

Convertendo tudo para coordenadas polares, nossa integral será:

∫ 0 π / 4 ∫ 0 2 ( r cos ⁡ θ + r   s e n   θ )   r   d r   d θ

Simplificando um pouco, ficamos com:

∫ 0 π / 4 ∫ 0 2 ( cos ⁡ θ +   s e n   θ )   r 2   d r   d θ

Passo 4

Vamos começar a integrar de dentro para fora. E tudo que não depende da variável de integração, é considerado uma constante.

∫ 0 π / 4 ( cos ⁡ θ +   s e n   θ ) ∫ 0 2 r 2   d r     d θ

Integrando em d r , vamos ter:

∫ 0 π / 4 ( cos ⁡ θ +   s e n   θ ) r 3 3 0 2     d θ

Aplicando os intervalos de integração:

∫ 0 π / 4 ( cos ⁡ θ +   s e n   θ ) 1 3 2 3 2 - 0     d θ

2 3 2 3 ∫ 0 π / 4 ( cos ⁡ θ +   s e n   θ ) d θ

Reescrevendo, temos:

2 3 2 3 ∫ 0 π / 4 cos ⁡ θ d θ + ∫ 0 π / 4   s e n   θ d θ

Agora temos uma integral simples em d θ . Integrando vamos ter:

2 3 2 3 s e n   θ - cos ⁡ θ 0 π / 4

Aplicando os limites de integração, ficamos com:

2 3 2 3 s e n π 4 - cos ⁡ π 4 - s e n   0 + cos ⁡ 0

Simplificando, temos:

2 3 2 3 1 2 - 1 2 - 0 + 1

2 3 2 3 ( 1 )

Logo, concluímos que nossa resposta é:

2 3 2 3 = 2 2 3

Resposta

2 2 3

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma região R é mostrada na figura. Decida se você deve usar coordenadas polares ou retangulares e escreva ∬ R f x , yd A como uma integral iterada, onde f é uma função qualquer contínua em R .
Calcule a integral dada, colocando-a em coordenadas polares. ∫ ∫ R x + yd A , onde R é a região que está a esquerda do eixo y e entre as circunferências x 2 + y 2 = 1 e x 2 + y 2 = 4 .
Calcule a integral dada, colocando-a em coordenadas polares.13. ∬ R a r c t gy xd A Onde R = x , y1 ≤ x 2 + y 2 ≤ 4 ,0 ≤ y ≤ x } .
Utilize a integral dupla para determinar a área da região.Um laço de rosácea r = cos ⁡ 3 θ .
Calcule a integral dada, colocando-a em coordenadas polares. ∬ De - x 2 - y 2d A , onde D é a região delimitada pelo semicírculo x = 4 - y 2 e o eixo y .