Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 15.4 - Ex. 31
Calcule a integral iterada, convertendo-a antes para coordenadas polares.
Passo 1
Faala, pessoal!
Nessa questão temos uma integral em coordenadas cartesianas e precisamos transformar para coordenadas polares e calcular.
Pra isso, vamos lembrar como fazemos essa mudança de coordenadas:
Sem esquecer do jacobiano!! Pra essa mudança é:
Então vamos começar desenhando o domínio dessa integral, pra conseguirmos redefinir em função de coordenadas polares.
Daí, vamos reescrever a integral iterada com as novas variáveis, e por fim calcular, de dentro pra fora.
Passo 2
Nossa integral é:
Pelos limites de integração de sabemos que:
Isso quer dizer que o domínio da nossa integral está entre as curvas:
Se elevarmos os dois lados da equação ao quadrado, vemos quem a duas representam a mesma curva:
Que é uma circunferência centrada na origem de raio . A diferença é que representa a circunferência para , e para .
Além disso, pelos limites de :
Ou seja, estamos só na parte positiva de .
Desenhando isso tudo temos:
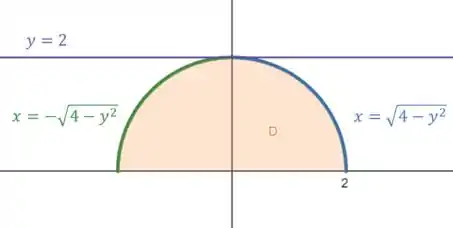
Passo 3
Agora vamos descrever essa região em coordenadas polares.
Como estamos nos dois primeiros quadrantes, usamos:
Já que o primeiro quadrante é a e o segundo é a .
Além disso, estamos em um círculo de raio , então:
Pra reescrever a integral, vamos mudar as variáveis do integrando.
Como e :
Colocando na integral temos:
Passo 4
Agora só falta calcular essa integral.
Fazemos de dentro pra fora. Primeiro em função de , considerando como constante:
Como é constante, pode sair dessa primeira integral:
Vamos mexer um pouco nesse integrando de . Já que ,
Além disso, podemos usar ,
Voltando pra integral:
Integrando:
Como :
Passo 5
Por último, integramos em função de :
Aplicando os limites de integração: