Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 15.3 - Ex. 39

Utilize coordenadas polares para combinar a soma

∫ 1 / 2 1 ∫ 1 - x 2 x x y     d y   d x + ∫ 1 2 ∫ 0 x x y     d y   d x + ∫ 2 2 ∫ 0 4 - x 2 x y     d y   d x

em uma única integral dupla. Em seguida calcule essa integral dupla.

Passo 1

Fala, pessoal! Tudo Joia?

A questão nos dá a soma de integrais em coordenadas retangulares:

∫ 1 / 2 1 ∫ 1 - x 2 x x y     d y   d x + ∫ 1 2 ∫ 0 x x y     d y   d x + ∫ 2 2 ∫ 0 4 - x 2 x y     d y   d x

E pede para que a gente transforme essa soma em somente uma integral dupla, utilizando coordenadas polares.

Olhando a soma de integrais, vemos que as três tem a mesma função a ser integrada.

f x , y = x y

O que muda são apenas as regiões sobre onde estão ocorrendo essa integração, já que cada uma das integrais tem seus próprios limites de integração.

Quando essas integrais se somam, é como se também pudéssemos “somar”, juntar as regiões de cada integração em uma região só.

Então, nossa primeira tarefa será achar a região de integração que representa a soma e expressar sua área por uma integral dupla usando as coordenadas polares.

Depois, finalizamos calculando o valor da integral!

Bora?

Passo 2

Vamos começar entendendo qual a região que está sendo descrita pela soma das 3 integrais.

  • ∫ 1 / 2 1 ∫ 1 - x 2 x x y     d y   d x :

    • x varia de 1 2 a 1 e y   varia de 1 - x 2 a x . Isso corresponde à parte do círculo x 2 + y 2 = 1 (raio = 1 ) que está entre y = 1 - x 2 e a reta y = x .

  • ∫ 1 2 ∫ 0 x x y     d y   d x :

    • x varia de 1 a 2 e y   varia de 0 a x . Isso corresponde à parte do círculo x 2 + y 2 = 2 (raio = 2 ) que está abaixo da reta y = x .

  • ∫ 2 2 ∫ 0 4 - x 2 x y     d y   d x :

    • x varia de 2 a 2 e y   varia de 0 a 4 - x 2 . Isso corresponde à parte do círculo x 2 + y 2 = 4 (raio = 2 ) que está abaixo da linha y = 4 - x 2 .

    Juntando tudo isso nessa figura, vamos entender que a região de integração é justamente a região sombreada:

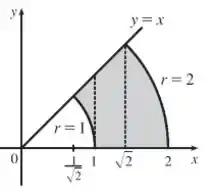
    A região sombreada na figura representa justamente a área total, enquanto as três áreas separadas por linhas pontilhadas são as regiões de cada integral da soma.

    Passo 3

    Agora precisamos expressar essa região em termos de coordenadas polares.

  • Os valores de r variam entre:

    • 1 ≤ r ≤ 2  

  • O ângulo parte do x no sentido anti-horário e para em meio quadrante, ou seja, π 4 .

0 ≤ θ ≤ π 4

Então, no final das contas, estamos integrando sobre 0 ≤ θ ≤ π 4   ,     1 ≤ r ≤ 2 :

∫ 1 / 2 1 ∫ 1 - x 2 x x y     d y   d x + ∫ 1 2 ∫ 0 x x y     d y   d x + ∫ 2 2 ∫ 0 4 - x 2 x y     d y   d x = ∫ 0 π / 4 ∫ 1 2 ( r cos ⁡ θ ) ( r   s e n   θ )     r   d r   d θ

Assim, conseguimos expressar toda a soma dada no enunciado como uma única integral dupla em coordenadas polares.

Passo 3

Show! Bora resolver a integral? Escrevemos a integral do produto como um produto de integrais:

∫ 0 π 4 ∫ 1 2 r 3 s e n θ cos ⁡ θ   d r   d θ = ∫ 0 π 4 s e n   θ cos ⁡ θ     d θ ∫ 1 2 r 3 d r

Resolvendo cada integral:

∫ 0 π 4 s e n   θ cos ⁡ θ     d θ ∫ 1 2 r 3 d r = s e n 2 θ 2 0 π 4 r 4 4 1 2

Aplicando os limites de integração de cada variável:

s e n 2 θ 2 0 π 4 r 4 4 1 2 = 1 2 1 2 2 - 0 2 1 4 16 - 1

Então, teremos por fim:

∫ 0 π 4 ∫ 1 2 r 3 s e n θ cos ⁡ θ   d r   d θ = 1 8   . 1 2   .   15 = 15 16

Resposta

15 16

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Encontre o valor médio da função f x , y = 1 / x 2 + y 2 na região anular a 2 ≤ x 2 + y 2 ≤ b 2 onde 0ab .
Calcule a integral dada, colocando-a em coordenadas polares. ∬ R sen ⁡ x 2 + y 2 d A Onde R é a região do primeiro quadrante entre os círculos com centro a origem e raios 1 e 3.
∬ D x 2 yd A , onde D é a metade superior do disco com centro na origem e raio 5.
Esboce a região cuja área é dada pela integral e calcule-a. ∫ π 3 π / 4 ∫ 1 2 rd rd θ
Seja D o disco com centro na origem e raio a. Qual é a distância média dos pontos em D em relação à origem?