Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 10.4 - Ex. 12
Esboce a curva e calcule a área limitada por ela.
Passo 1
Fala galerinha. Tranquilo?
A questão pede para encontrar a área da região limitada pela curva .
Vamos calcular a Área através de uma fórmula. Assim que resolve-la, obtemos o resultado. Se liga nos passos, Será moleza!
- Utilizar a equação da área, com o intervalo de integração fornecido.
- Descobrir os limites de integração.
- Calcular a área.
É isso pessoal! Agora é só calcular!
Passo 2
Vamos primeiro determinar os limites de integração.
A equação descreve uma curva simétrica em relação ao eixo polar. O termo atinge seu valor máximo em e retorna a zero em . Assim, uma pétala é formada no intervalo .
Temos que lembrar que devido a simetria, basta calcular a área de uma pétlada e multiplicar pelo número total de pétalas. Significa então que integrando de a estamos pegando apenas uma pétala, multiplicando por obtemos a área total da curva.
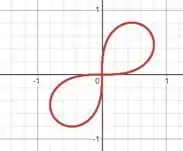
Sendo assim o intervalo de integração é:
Passo 3
Para calcular a área, vamos considerar apenas um laço e no final multiplicar por dois:
Fazendo a integração,
Passo 4
Como a área pedida é o dobro da área de um laço:
Portanto,