Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 15.7 - Ex. 13

Calcule a integral iterada.

∭ E x 2 e y   d V , onde E é limitado pelo cilindro parabólico z = 1 - y 2 e pelos planos z = 0 , x = 1 e x = - 1 .

Passo 1

E aii, pessoal!

Essa questão pede pra gente calcular uma integral tripla sobre um sólido E que ele descreveu

∭ E x 2 e y   d V

Pra isso, vamos primeiro esboçar a região E pra definir os limites de integração.

Assim conseguimos transformar a integral em uma integral iterada e calcular.

Passo 2

O sólido E é limitado pelo cilindro

z = 1 - y 2

Que é uma parábola no plano y z .

Além disso, pelo plano z = 0 (plano x y ) e pelos planos:

x = 1 ,   x = - 1

Vamos desenhar:

(em vermelho o cilindro parabólico e em azul os planos x = ± 1 )

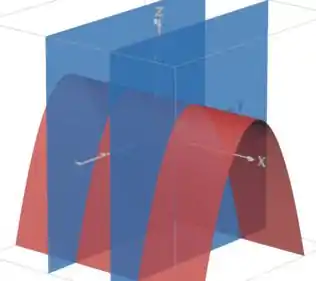
Então o sólido fica assim:

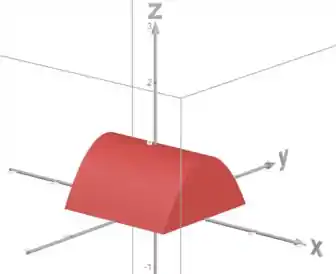
Para definir os limites de z , vemos que o sólido está entre o plano z = 0 e o cilindro z = 1 - y 2 , então:

0 ≤ z ≤ 1 - y 2

Passo 3

Para os limites de x e y , vamos ver a projeção do sólido no plano x y :

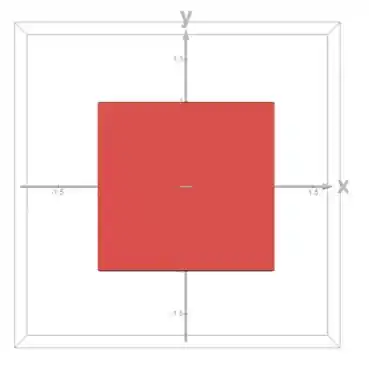
Como a projeção é um quadrado, temos:

- 1 ≤ x ≤ 1

- 1 ≤ y ≤ 1

Agora podemos transformar a integral em uma integral iterada!

Só que como os limites de z dependem de y , temos que integrar primeiro em função de z , depois de y .

A integral fica assim:

∭ E x 2 e y   d V = ∫ - 1 1 ∫ - 1 1 ∫ 0 1 - y 2 x 2 e y d z d y d x

Passo 4

Começamos integrando em função de z , considerando x e y como constantes:

∫ - 1 1 ∫ - 1 1 ∫ 0 1 - y 2 x 2 e y d z d y d x =

Podemos tirar x 2 e y dessa primeira integral, por ser constante:

= ∫ - 1 1 ∫ - 1 1 x 2 e y ∫ 0 1 - y 2 d z d y d x =

= ∫ - 1 1 ∫ - 1 1 x 2 e y z z = 0 z = 1 - y 2 d y d x =

Substituindo os limites de integração:

= ∫ - 1 1 ∫ - 1 1 x 2 e y 1 - y 2 - 0 d y d x =

= ∫ - 1 1 ∫ - 1 1 x 2 e y - y 2 e y d y d x =

Passo 5

Agora vamos integrar em função de y :

= ∫ - 1 1 ∫ - 1 1 x 2 e y - y 2 e y d y d x =

Primeiro tiramos o x 2 dessa integral, por ser constante:

= ∫ - 1 1 x 2 ∫ - 1 1 e y - y 2 e y d y d x =

Pra integrar isso, vamos calcular a primitiva de y 2 e y separado:

∫ y 2 e y d y

Vamos usar integração por partes

u = y 2 ⇒ d u = 2 y d y

d v = e y d y ⇒ v = e y

Então:

∫ y 2 e y d y = y 2 e y - ∫ 2 y e y d y

Integrando por partes de novo:

u = 2 y ⇒ d u = 2 d y

d v = e y d y ⇒ v = e y

Então:

∫ y 2 e y d y = y 2 e y - 2 y e y - ∫ 2 e y d y

∫ y 2 e y d y = y 2 e y - 2 y e y + 2 e y

Voltando pra integral: = ∫ - 1 1 x 2 ∫ - 1 1 e y - y 2 e y d y d x =

= ∫ - 1 1 x 2 e y - y 2 e y - 2 y e y + 2 e y y = - 1 y = 1 d x =

Reescrevendo:

= ∫ - 1 1 x 2 - y 2 e y + 2 y e y - e y y = - 1 y = 1 d x =

Aplicando os limites de integração:

= ∫ - 1 1 x 2 ∙ - e + 2 e - e - - e - 1 - 2 e - 1 - e - 1 d x =

= ∫ - 1 1 x 2 ∙ 4 e - 1 d x =

Passo 6

Por último, vamos integrar em função de x :

= ∫ - 1 1 x 2 ∙ 4 e - 1 d x =

= 4 e - 1 ∫ - 1 1 x 2 d x =

Integrando:

= 4 e - 1 x 3 3 - 1 1 =

= 4 e - 1 1 3 - - 1 3 = 4 e - 1 ∙ 2 3

Então:

∭ E x 2 e y   d V = 8 3 e

Resposta

∭ E x 2 e y   d V = 8 3 e

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Use a integral tripla para determinar o volume do sólido dado.O sólido limitado pelo cilindro x 2 + y 2 = 9 e pelos planos y + z = 5 e x = 1 .
Calcule a integral tripla ∭ E x d V Onde E é limitado pelo parabolóide x = 4 y 2 + 4 z 2 e pelo plano x = 4
Esboçar a região de integração e calcular as integrais:g) ∫ 0 2 ∫ 0 1 2 4 - x 2 ∫ 0 x 2 + 4 y 2 d z d y d x
Esboçar a região de integração e calcular as integrais:h) ∫ - 3 3 ∫ - 9 - y 2 9 - y 2 ∫ 4 x 2 + 4 y 2 - 9 3 x 2 + 3 y 2 d z d x d y
Calcular a integral tripla dada sobre a região indicada ∫ ∫ ∫ T d V Onde T é a região delimitada por x=y 2 ,y = x 2 ,z = 2 y ,z = - 2 y .