Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 15.Revisão - Ex. 13

Calcule a integral iterada, primeiro invertendo a ordem de integração.

∫ 0 1 ∫ x 1 cos ⁡ y 2   d y   d x

Passo 1

E aí meus queridxs, tudo bom com vocês? Vamos lá, precisamos calcular a integral iterada acima, no entanto, a questão pede primeiramente que invertamos a ordem de integração, para isso precisamos descrever a região que estamos integrando que pode ser descrita como

x , y |   0 ≤ x ≤ 1 ,   x ≤ y ≤ 1

Graficamente essa região é dada por

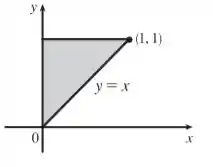
Passo 2

Agora que temos a região podemos inverter a ordem de integração ficando com

∫ 0 1 ∫ x 1 cos ⁡ y 2   d y   d x = ∫ 0 1 ∫ 0 y cos ⁡ y 2   d x   d y

Resolvendo a integral mais interna vamos ficar com

∫ 0 y cos ⁡ y 2   d x = x ⋅ cos ⁡ y 2 0 y = y ⋅ cos ⁡ y 2

Agora, ficamos com a seguinte integral simples

∫ 0 1 y ⋅ cos ⁡ y 2   d y

Para resolvermos essa integral vamos utilizar a seguinte substituição simples

u = y 2 → d u d y = 2 y → d u 2 = y   d y

Onde quando y = 1 → u = 1 e quando y = 0 → u = 0 . Assim, teremos

∫ 0 1 cos ⁡ u 2   d y = s e n u 2 0 1 = s e n 1 2

Pronto, tá resolvida nossa questão.

Resposta

s e n 1 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Nos Exercícios 1-12, calcule a integral iterada.
Nos Exercícios 1-12, calcule a integral iterada.
Nos Exercícios 9-22, substitua a integral cartesiana por uma integral equivalente. Em seguida, calcule a integral polar. ∫ 1 3 ∫ 1 x d yd x
Reduzindo uma integral dupla a simples Mudando a ordem de integracao, mostre que a integral dupla a seguir pode ser reduzida para uma integral simples: ∫ 0 x ∫ 0 u e m x - t f t d td u =∫ 0 x x - t e
Calcule a integral ∫ 0 ∞ e - a x - e - b x x d x (Sugestao: utilize a relação: e - a x - e - b x x = ∫ a b e - x y d y para formar uma integral dupla e calcule a integral mudando a ordem de integração