Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 15.Revisão - Ex. 19
Calcule o valor da integral múltipla.
onde é a região no primeiro quadrante limitada pelas parábolas
Passo 1
E aí galerinha, tudo bem?! Vamos nessa!!
Precisamos calcular o valor da seguinte integral:
onde é a região no primeiro quadrante limitada pelas parábolas:
O primeiro passo é fazer um esboço das curvas para conhecer nossa região, pode usar o Geogebra para você ter uma precisão.
Ai vamos comparar o gráfico com as regiões de integração do Tipo I e II. E ver se podemos utilizar alguma das duas para montar nossa integral.
Região Tipo I tem essa cara:
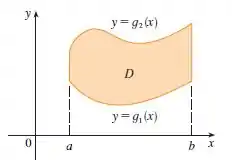
Já a região Tipo II:
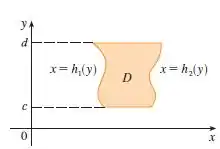
Feito essa comparação e definido o tipo de região, é só montar e resolver a integral.
Bora lá!!
Passo 2
Sabemos que a região está no primeiro quadrante limitada pelas parábolas .
Utilizando o Geogebra como apoio para termos um gráfico preciso, obtemos:
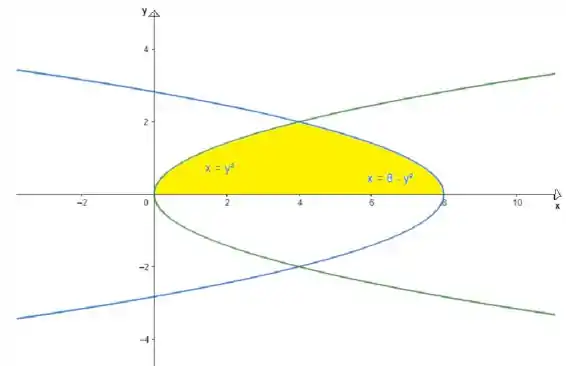
Repare que nossa região de interesse é somente a pintada em amarelo, porque queremos apenas no primeiro quadrante.
Observando e comparando com as regiões tipo I e II, temos que essa região é do tipo II:
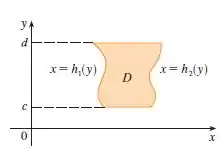
Logo, nossos intervalos de integração são:
Assim, conseguiremos reescrever nossa integral como sendo:
Passo 3
Sabemos como é nossa integral:
Agora vamos começar a integração, lembrando que começamos de dentro para fora.
Integrando em , vamos ter:
Aplicando os limites de integração, ficamos com:
Simplificando, temos:
Agora, ficamos com a seguinte integral simples a ser resolvida. Integrando em , temos:
Aplicando os limites de integração:
Assim, nossa resposta é: