Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 15.Revisão - Ex. 47
Reescreva a integral
Como uma integral iterada na ordem .
Passo 1
Faaaaaala meus queridos, tudo na paz com vocês?! Bora lá!
Nossa missão é reescrever a seguinte integral:
Como uma integral iterada na ordem .
Vamos pensar juntos um pouco, beleza?
Olhando para os intervalos de integração, temos que nossa região de integração é a seguinte:
Lembra que sempre integramos primeiro os termos que tem função nos limites, e o ultimo vai depender apenas de valores numéricos.
Essa é a ordem de integral que queremos determinar:
Sabemos pela ordem de integração que a variação em e vão depender de funções, já em de valores numéricos.
Esse vai ser nosso objetivo, escrever as variáveis em função das outras. E para isso vai te ajudar muito fazer um esboço gráfico das regiões, utilize um software gráfico de sua preferência.
Porque utilizar um gráfico? Porque você vai entender o comportamento da função com precisão.
Vamos nessa!!!
Passo 2
Vamos começar analisando nossos intervalos de integração.
Desses intervalos podemos concluir que:
E,
Fazendo o gráfico para ter uma maior precisão das curvas, temos que:
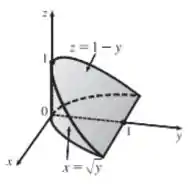
Agora, quero que você olhe para o plano . Perceba que vamos ter a seguinte imagem:
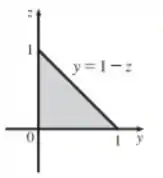
Dessa imagem podemos dizer que:
Já determinamos os intervalos do eixo e , agora estamos interessados no eixo . Repare que no eixo a variação é de:
Agora, temos as informações para montar a integral. Vamos nessa!!!
Passo 3
Já temos os novos intervalos de integração, que são:
E nosso objetivo é escrever na ordem:
Substituindo na integral, vamos ter:
Ambas as integrais tem a mesma resposta, só estão escritas em outras variáveis.