Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 15.3 - Ex. 55

Calcule a integral

∬ D x 2   t g   x + y 3 + 4   d A ,

onde D = x , y   x 2 + y 2 ≤ 2 } . [Sugestão: explore o fato de que D é simétrica com relação a ambos os eixos.]

Passo 1

E aí futuro cientista, preparado para usar todo seu talento em cálculo nessa questão de matemática? Vamos arrebentar!

Para resolver a integral ∬ D x 2   t g   x + y 3 + 4   d A , onde D é a região delimitada pelo círculo de raio 2 , vamos utilizar a simetria do problema. A região D é simétrica em relação aos eixos x e y , o que nos permite simplificar a resolução da integral.

A região de integração é a região interna ao círculo de raio 2 , centrado na origem. Esse círculo é simétrico em relação aos eixos x e y , o que nos permitirá simplificar a integral ao notar que algumas funções integradas são ímpares.

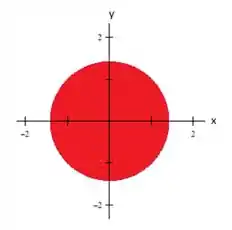
Note que a questão pede para usarmos a simetria do problema para calcular a integral!

Observe que como a tangente é uma função ímpar, x 2   t g   x é uma função ímpar na variável x . Assim, a parte da integral que envolve essa função será nula, pois o intervalo de integração é simétrico em x :

∬ D x 2   t g   x   d A = 0

Analogamente, como y 3 é ímpar, temos que

∬ D y 3   d A = 0

Assim,

∬ D x 2   t g   x + y 3 + 4   d A = ∬ D x 2   t g   x   d A + ∬ D y 3   d A + 4 ∬ D d A

= 4 ∬ D d A

Passo 2

Por outro lado, a integral que resta é simplesmente a área do círculo de raio 2 , ou seja, a integral da função constante 1 sobre a região D :

∬ D d A = Área da região D

Como D é o círculo de raio 2 , a área A de círculo é dada pela fórmula A = π r 2 . Aqui, r = 2 , então a área é:

A = π 2 2 = 2 π

Portanto, a integral da unidade sobre a região D é a área do círculo, 2 π :

∬ D d A = 2 π

Substituindo este valor na integral simplificada, temos:

∬ D d A = 4 ⋅ 2 π = 8 π

Resposta

8 π

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Nos Exercícios 1-12, esboce a região delimitada pelas retas e curvas dadas. Em seguida, expresse a área da região como uma integral dupla iterada e calcule a integral. a sp a r á b o l a sx = y 2 - 1e
As integrais e somas de integrais nos Exercícios 13-18 fornecem as áreas das regiões no plano xy. Esboce cada região, marque cada curva limitante com sua equação e forneça as coordenadas dos pontos on
Avalie a integral:int_0^2 int_((y)/(2))^1 e^(x^2) d x d y
Avalie a integral:int_0^1 int_(root(3)(y))^1 (2 pi s e n ( pi x^2 ))/(x^2) d x d y
Avalie a integral:int_0^8 int_(root(3)(x))^2 (1)/(y^4 + 1) d y d x