Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 16.7 - Ex. 19
Calcule a integral de superfície.
é a parte do cilindro que está entre os planos e no primeiro octante
Passo 1
E aii meu povo, beleza!?
Precisamos calcular a seguinte integral de superfície:
Onde,
é a parte do cilindro que está entre os planos e no primeiro octante.
Vamos primeiro fazer um esboço da região S para entender a região. Utilizando o Geogebra, temos:
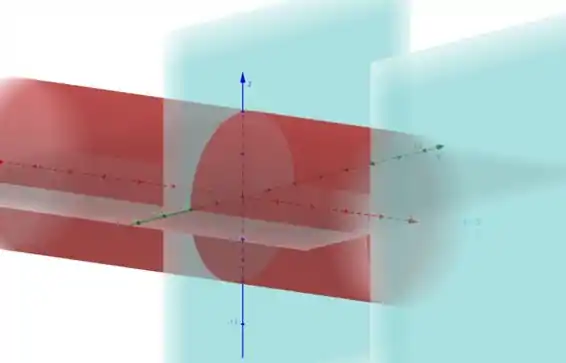
Em vermelho temos o cilindro e em azul os planos, e nossa região de interesse é a parte do cilindro que está entre os dois planos. Mas uma observação, ai temos a figura nos 8 octantes.
Para esse tipo de situação, é mais fácil definirmos uma parametrização para a superfície e calcular a seguinte integral de superfície:
Onde, é a nossa parametrização. Observe que temos um círculo de raio no plano , logo podemos usar coordenadas polares:
E para um octante, temos:
Dessa forma, podemos escrever a parametrização assim:
Agora, você precisa fazer as derivadas de em relação a e e encontrar o modulo do produto vetorial. Feito isso, e só substituir tudo na integral e resolvê-la.
Vamos nessa pessoal!
Passo 2
Vamos começar encontrando o termo da integral:
Já sabemos que nossa parametrização é:
Fazendo as derivadas parciais, vamos ter:
Agora vamos aplicar o produto vetorial:
Resolvendo como um determinante, vamos ter:
Aplicando o módulo, que é fazer a raiz da soma dos termos ao quadrado vamos ter:
Assim, podemos escrever a integral:
Agora é só parametrizar , substituindo vai ficar assim:
Substituindo tudo na integral, ficamos com:
Passo 3
Show ein pessoal, mandaram bem até aqui!
Agora vamos resolver a integral:
Integrando em , vamos ficar com:
Aplicando os limites de integração, ficamos com:
Agora ficamos com uma integral simples em , e integrando vamos ter:
Aplicando os limites de integração, temos:
Assim, concluímos que a resposta é: