Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diva Flemming - Cálculo B - Ed: 2º - Capítulo 10.11 - Ex. 41 - c

Uma superfície S é representada pela equação vetorial r →   u , v   = 4 cos ⁡ u ,       4 s e n   u   ,       4 v

0 ≤ u ≤ 2 π

0 ≤ v ≤ 2

  1. Determinar a equação cartesiana de S
  2. Desenhar sobre a superfície S as curvas coordenadas obtidas fixando u = π 3 e v   =   1 , respectivamente
  3. Determinar o vetor ∂ r → ∂ u   x ∂ r → ∂ v   no ponto em que u = π 3 e v = 1 , representando -o no correspondente ponto P de S
  4. Supondo que uma lamina de densidade constante é representada por r →   u , v ,   determine o momento de inercia da lamina em relação ao eixo z

Passo 1

  1. Determinar o vetor ∂ r → ∂ u   x ∂ r → ∂ v   no ponto em que u = π 3 e v = 1 , representando -o no correspondente ponto P de S

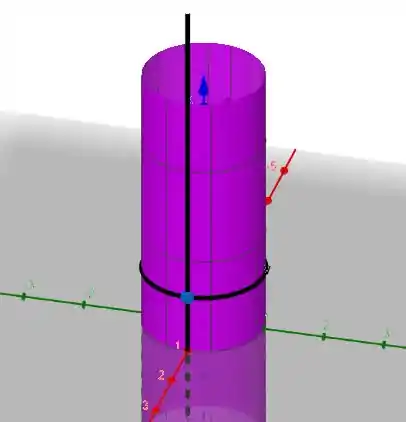
Representei o ponto geometricamente. Vamos Calcular ∂ r → ∂ u   x ∂ r → ∂ v

Primeiro calculando as parciais

r u = - 4 s e n u , 4 c o s u , 0  

r v = 0,0 , 4

∂ r ∂ u   x ∂ r ∂ v =   x → y → z → - 4 s e n   u   4 cos ⁡ u 0 0 0 4

∂ r → ∂ u   x ∂ r → ∂ v = 16 cos ⁡ u ,   16 s e n   u , 0  

Considerando que o ângulo é u = π 3

∂ r → ∂ u   x ∂ r → ∂ v = 8 ,   8 3   , 0

Terminamos por aqui. Te vejo na próxima resolução

: )

Resposta

∂ r → ∂ u   x ∂ r → ∂ v = 8 ,   8 3   , 0

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule a integral de superfície. ∫ ∫ S x 2 y + z 2 d S S é a parte do cilindro x 2 + y 2 = 9 entre os planos z = 0 e z = 2 .
Calcule a integral de superfície. ∫ ∫ S x y zd S , S é a parte da esfera x 2 + y 2 + z 2 = 1 que está acima do cone z = x 2 + y 2 .
Determine a área de superfície.A parte do plano x + 2 y + z = 4 que está dentro do cilindro x 2 + y 2 = 4 .
Encontre a área da superfície com precisão de quatrocasas decimais, expressando-as em termos de uma integral de função de uma variável real e usando sua calculadora para estimar a integral.A parte da
Use a regra do ponto médio para as integrais duplas (veja a Seção 15.1) com quatro quadrados para estimar a área de superfície da parte do paraboloide z = x 2 + y 2 que está acima do quadrado 0,1 × [