Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 16.6 - Ex. 63

Encontre a área da parte da esfera x 2 + y 2 + z 2 = a 2 que está dentro do cilindro x 2 + y 2 = a x .

Passo 1

Fala aê, pessoal! Tudo show?

Precisamos, como pede o enunciado, calcular a área da intersecção de parte da esfera

x 2 + y 2 + z 2 = a 2

Que está dentro do cilindro

x 2 + y 2 = a x

Assim, ó:

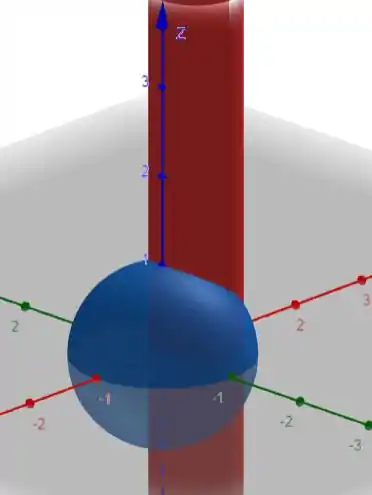
Pra gente calcular a área de superfície, temos essa fórmula aqui:

A S = ∫ ∫ D 1 + ∂ z ∂ x 2 + ∂ z ∂ y 2 d A

Onde precisamos calcular as derivadas parciais dentro da raiz e fazer a festa acontecer.

Passo 2

Primeiro, quem é esse z ?

Simples! Pegamos nossa esfera definida pela equação dada pelo enunciado e isolamos o z :

x 2 + y 2 + z 2 = a 2

z = a 2 - x 2 - y 2

Com isso, fazemos as derivadas parciais de z em relação a x e a y :

∂ z ∂ x a 2 - x 2 - y 2 → - 2 x 2 a 2 - x 2 - y 2

∂ z ∂ y a 2 - x 2 - y 2 → - 2 y 2 a 2 - x 2 - y 2

Podemos melhorar essas equações:

- 2 x 2 a 2 - x 2 - y 2 ⏟ z → - x z

- 2 y 2 a 2 - x 2 - y 2 ⏟ z → - y z

Desse jeito, jogando na fórmula, teremos:

A S = ∫ ∫ D 1 + - x z 2 + - y z 2 d A

Organizando os termos dentro da raiz:

A S = ∫ ∫ D 1 + x 2 z 2 + y 2 z 2 d A

Colocando todos sobre o mesmo denominador:

A S = ∫ ∫ D x 2 + y 2 + z 2 z 2 d A

Substituindo o valor de z que conhecemos:

A S = ∫ ∫ D a a 2 - x 2 - y 2 d A

Passo 3

Jogando tudo pras coordenadas polares, teremos

x = r c o s θ

y = r s e n θ

z = z

r 2 = x 2 + y 2

d A = r d r d θ

Sabemos que o cilindro é dado por

x 2 + y 2 = a x

Ou seja, o raio é

r 2 = a   r c o s θ

Dividindo os dois termos por r , teremos:

r = a c o s θ

Então, nas coordenadas, para uma porção da esfera acima do plano z = 0 , encontraremos nossos limites de integração como

0 ≤ r ≤ a c o s θ

- π 2 ≤ θ ≤ π 2

Passo 4

Show! Com todas essas informações, podemos montar nossa integral e resolvê-la.

A S = ∫ - π 2 π 2 ∫ 0 a c o s θ a a 2 - x 2 - y 2 r d r d θ

Como sabemos que

x 2 + y 2 = r 2

Então:

A S = ∫ - π 2 π 2 ∫ 0 a c o s θ a a 2 - r 2 r d r d θ

Resolvendo a integral de dentro para fora, teremos:

∫ - π 2 π 2 - a a 2 - r 2 0 a c o s θ d θ

Substituindo os limites de integração:

∫ - π 2 π 2 - a 2 s e n 2 θ - - a 2 d θ

Como estamos trabalhando com uma área completa, e não com um hemisfério dessa região, então podemos calcular um desses hemisférios e multiplicar por 2 , tendo então:

2 ∫ 0 π 2 a 2 - a 2 s e n θ   d θ

Resolvendo e pondo os limites de integração, chegaremos a

2 a 2 θ + c o s θ 0 π 2 = 2 a 2 ( π - 2 )

Show de bola! 😊

Resposta

A S = 2 a 2 ( π - 2 )

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

4 . Calcule a área da parte da superfície cilíndrica z 2+x 2=4 que seencontra dentro do cilindro x 2+y 2≤4 e acima do plano xy
10 . Calcule a área de z = sqrt(x^2 + y^2) , x^2 + y^2 = 2 x , x = 1 e y = 0
8 . Calcule a área da parte do cone z 2=x 2+y 2 que se encontra dentro docilindro x 2+y 2≤2 x , fora do cilindro x 2+y 2≤1 e acima do plano x y .
Calcule a área da parte do paraboloide elíptico z = x 2 + 2 y 2 que se encontra dentro do cilindro 4 x 2 + 16 y 2 ≤ 1 .
Seja K o conjunto do plano x y limitado pelas curvas (em coordenadas polares) ρ = t gθ , 0θπ 2 ,eθ = π 4 . Calcule a área da superfície z = x y , x , y ∈ K .