Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 16.6 - Ex. 58

(a) Determine, mas não calcule, a integral dupla da área da superfície com as equações paramétricas

x = a   u cos ⁡ v   ,       y = b   u   s e n   v   ,       z = u 2   ,           0 ≤ u ≤ 2   ,       0 ≤ v ≤ 2 π

(b) Elimine os parâmetros para mostrar que a superfície é um paraboloide elíptico e escreva outra integral dupla que forneça sua área.

(c) Use as equações paramétricas da parte (a) com a = 2 e b = 3 para traçar o gráfico da superfície.

(d) Para o caso a = 2   ,     b = 3   , use um sistema de computação algébrica para achar a área da superfície com precisão de quatro casas decimais.

Passo 1

E aí, meus terráqueos. Aqui quem fala é a nave-mãe pra gente resolver umas questões casca de bala!

No item (a), precisamos determinar, sem calcular absolutamente nadica de nada, a integral dupla da área de superfície parametrizada com esses dados aqui:

x = a   u cos ⁡ v   ,       y = b   u   s e n   v   ,       z = u 2   ,           0 ≤ u ≤ 2   ,       0 ≤ v ≤ 2 π

No item (b), não usar mais os parâmetros, e mostrar que a superfície é um paraboloide elíptico, definindo outra integral dupla para a área de superfície.

No item (c), queremos traçar um gráfico usando parametrizações do item (a), substituindo a = 2 e b = 3 .

Já no item (d), achar o resultado exato da área de superfície usando um software top para os valores de a e b do item (c).

Passo 2

(a) Galera, a gente tem uma função r definida por

r = x i + y j + z k

Então, com as nossas informações temos:

r = a   u cos ⁡ v i + b   u   s e n   v   j + u 2   k

A integral para encontrar a área de superfície é dada por

A S = ∫ ∫ D | r u × r v | d A

Com isso, precisamos fazer as derivadas parciais de r em relação a u e a v e depois o produto vetorial entre eles:

r u = a cos ⁡ v i + b   s e n   v   j + 2 u   k

r v = - a u   s e n   v   i + b u cos ⁡ v j + 0   k

r u × r v = i j k a cos ⁡ v b   s e n   v 2 u - a u   s e n   v b u cos ⁡ v 0

Chegaremos, pelo método de Sarrus (cálculo das diagonais) ou por qualquer outro que você queira, a esse resultado:

- 2 b u 2 cos ⁡ v i - 2 a u 2   s e n   v   j + a b u   k

O módulo será calculado como a soma de cada termo ao quadrado dentro da raiz:

4 b 2 u 4 cos 2 ⁡ v + 4 a 2 u 4   s e n 2   v + a 2 b 2 u 2

Com os limites de integração iguais a

0 ≤ u ≤ 2   ,       0 ≤ v ≤ 2 π

Podemos escrever a integral dupla da área da superfície assim:

∫ 0 2 π ∫ 0 2 4 b 2 u 4 cos 2 ⁡ v + 4 a 2 u 4   s e n 2   v + a 2 b 2 u 2 d u   d v

Passo 3

No item (b), perceba o seguinte. Para um paraboloide elíptico, temos que

x 2 = a 2 u 2 cos 2 ⁡ v   ,       y 2 = b 2 u 2   s e n 2   v

Já que a fórmula gerla para essa figura é dada por

x 2 a 2 + y 2 b 2 = u 2 = z

Ou seja, a superfície é realmente um paraboloide elíptico, e

0 ≤ u ≤ 2

0 ≤ z ≤ 4

0 ≤ x 2 a 2 + y 2 b 2 ≤ 4

Então, podemos ver a superfície como o gráfico de uma função

z x ,   y = x 2 a 2 + y 2 b 2

e aí a área da superfície seria dada pela fórmula:

A S = ∫ ∫ D 1 + ∂ z ∂ x 2 + ∂ z ∂ y 2   d A

onde D seria a região

0 ≤ x 2 a 2 + y 2 b 2 ≤ 4

Ou seja, podemos escrever a integral assim, lembrando de calcular as derivadas parciais de z dentro da raiz:

A S = ∫ - 2 a 2 a ∫ - b 4 - x 2 a 2 b 4 - x 2 a 2 1 + 2 x a 2 2 + 2 y b 2 2   d y   d x

Passo 4

No item (c), vamos usar as equações paramétricas com a = 2 e b = 3 para traçar o gráfico da superfície, com o paraboloide

z = x 2 a 2 + y 2 b 2

Ou melhor,

z = x 2 4 + y 2 9

Jogando no programa, chegaremos a

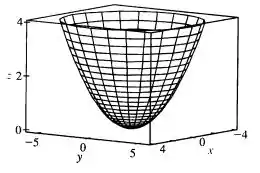
Passo 5

Agora no item (d), substituindo a = 2 e b = 3 na integral que obtivemos no item (a), e utizando um CAS para estimar a integral, teremos:

A S = ∫ 0 2 π ∫ 0 2 2 u 9 u 2 cos 2 ⁡ v + 4 u 2   s e n 2   v + 9 d u   d v ≈ 115,6596

Resposta

a   A S = ∫ 0 2 π ∫ 0 2 4 b 2 u 4 cos 2 ⁡ v + 4 a 2 u 4   s e n 2   v + a 2 b 2 u 2 d u   d v

b   A S = ∫ - 2 a 2 a ∫ - b 4 - x 2 a 2 b 4 - x 2 a 2 1 + 2 x a 2 2 + 2 y b 2 2   d y   d x

c

d   A S ≈ 115,6596

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Seja K o conjunto do plano x y limitado pelas curvas (em coordenadas polares) ρ 2 = cos ⁡ 2 θ , - π 4 ≤ θ ≤ π 4 ,eθ = π 4 . Calcule a área da superfície z = x y , x , y ∈ K .
Calcule ∬_K f (x , y , z) d S sendo:f (x , y , z) = x ; sigma (u , v) = (u , v , u^2 + v) , 0 = u = 1 e u^2 = v = 1 .
Calcule ∬ K f x , y , z d S sendo: g )f x , y , z = z ;σ é a parte da superfície z 2 = x 2 + y 2 que se encontra acima do paraboloide 4 z = x 2 + y 2 + 3 .
Calcule ∬ K f x , y , z d S sendo: i )f x , y , z = 1 - x 2 ;σ é a parte da superfície cilíndrica z 2 + x 2 = 1 que se encontra dentro do cone z ≥ x 2 + y 2 .
Calcule ∬ K f x , y , z d S sendo: i )f x , y , z = z 1 + 4 x 2 + 4 y 2 ;σ é a parte do paraboloide z = 1 - x 2 - y 2 que se encontra dentro do cilindro x 2 + y 2 ≤ 2 y .