Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 15.9 - Ex. 31

(a) Encontre o centroide do sólido no Exemplo 4 .

(b) Encontre o momento de inércia em torno do eixo z para este sólido.

Passo 1

Vamos lá galerinha, temos que o centroide e o momento de inércia do sólido:

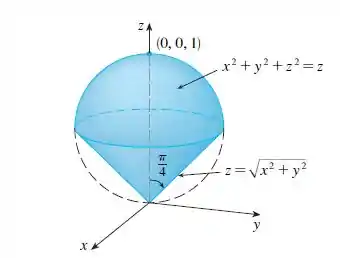
Ou seja, iremos utilizar a equação do corpo acima e inserir nas respectivas equações de centroide e de momento de inércia.

Vamos lembrar como se calcula um centroide? Ele é o ponto no qual todo corpo está em equilíbrio, e as coordenadas desse ponto são:

x , y , z = M y z m , M x z m , M x y m

Certo?

Por simetria sabemos que M y z = M x z = 0 e sabemos também que K é constante. Então precisamos calcular m e M x y . Começando pela massa m . A massa é a integral da densidade sobre todo volume, e conforme calculado no exemplo temos que a massa é:

m = ∭ E K d V = π 8 K

Passo 2

Agora vamos calcular M x y e ele é dado por:

M x y = ∭ E z K   d V

Os limites de integração são os mesmos do exemplo, pois estamos falando do mesmo sólido então resgatando de lá os limites (em coordenadas esféricas) temos:

0 ≤ ρ ≤ c o s ϕ 0 ≤ θ ≤ 2 π 0 ≤ ϕ ≤ π / 4

E a relação entre as coordenadas esféricas e a coordenada z é:

z = ρ c o s ϕ

E o diferencial de volume é ρ 2 s e n ϕ   d ρ   d ϕ   d θ , então agora que temos tudo podemos montar a integral e começar a calcular ela:

M x y = K ∫ 0 2 π ∫ 0 π / 4 ∫ 0 c o s ϕ ρ c o s ϕ . ρ 2 s e n ϕ   d ρ   d ϕ   d θ  

Vamos começar integrando na variável ρ :

M x y = K ∫ 0 2 π d θ ∫ 0 π / 4 s e n ϕ ρ 4 4 0 c o s ϕ d ϕ = K 4 ∫ 0 2 π d θ ∫ 0 π / 4   s e n ϕ cos 5 ⁡ ϕ d ϕ

Agora vamos integrar na variável ϕ :

M x y = K 4 ∫ 0 2 π - cos 6 ⁡ ϕ 6 0 π / 4 d θ = K 4 - cos ⁡ π 4 6 6 - - cos ⁡ 0 6 6 ∫ 0 2 π d θ

Agora antes de ir pra integração em θ vou simplificar esses colchetes:

M x y = K 4 . 1 6   - 2 2 6 + 1 ∫ 0 2 π d θ = K 24 - 1 8 + 1 ∫ 0 2 π d θ = K 24   . 7 8 ∫ 0 2 π d θ

Agora sim vou fazer a integral em θ :

M x y = K 24 . 7 8 . θ 0 2 π = K 24 . 7 8 . 2 π = 7 K 96

Beleza!

Passo 3

Agora com os resultados de m e de M x y (lembrando que M x z = M y z = 0 )vamos determinar o centroide:

x , y , z = M y z m , M x z m , M x y m = 0,0 , 7 K π 96 π 8 K   = 0,0 , 7 12

Passo 4

Letra b:

O momento de inércia em torno do eixo z vai ser:

I z = ∭ r 2 K d V

Onde r 2 é a distância do centroide até o eixo d rotação. Sabemos que x 2 + y 2 = z 2 , e em coordenadas esféricas z 2 = ρ 2 s e n 2 ϕ . Então nossa expressão para o momento de inércia é:

I z = ∭ E ρ 2 s e n 2 ϕ   K   d V

Passo 5

Mas quais serão os limites de integração? Ora, estamos falando do mesmo sólido! Então os limites de integração são os mesmos do passo 2 , bem como o diferencial de volume! Resgatando esses valores nossa integral fica assim:

I z = K ∫ 0 2 π ∫ 0 π / 4 ∫ 0 c o s ϕ ρ 4 s e n 3 ϕ   d ρ   d ϕ   d θ  

Vamos primeiro integrar em ρ :

I z = K ∫ 0 2 π d θ ∫ 0 π / 4 s e n 3 ϕ ρ 5 5 0 c o s ϕ d ϕ = K 5 ∫ 0 2 π d θ ∫ 0 π / 4   s e n 3 ϕ cos 5 ⁡ ϕ d ϕ

Vou usar um truque sujo! Vou substituir s e n 2 ϕ por 1 - cos 2 ⁡ ϕ e daí conseguimos integrar bem facinho, sem a ajuda de uma tabela, saca só:

I z = K 5 ∫ 0 2 π d θ ∫ 0 π 4 1 - cos 2 ⁡ ϕ cos 5 ⁡ ϕ s e n ϕ   d ϕ

Fazendo a distributiva:

= K 5 ∫ 0 2 π d θ ∫ 0 π / 4 cos 5 ⁡ ϕ - cos 7 ⁡ ϕ s e n ϕ   d ϕ

Agora sim podemos integrar em ϕ :

I z = K 5 ∫ 0 2 π d θ - 1 6 c o s ϕ 6 + 1 8 c o s ϕ 8 0 π / 4 = K 5 - 1 6 2 2 6 + 1 8 2 2 8 + 1 6 - 1 8 ∫ 0 2 π d θ

A integral de d θ é θ e avaliada nos limites temos ( 2 π - 0 ) , então vou pular essa partezinha e só multiplicar por 2 π tá? E simplificar aqueles colchetes:

I z = 2 π K 5 - 1 48 + 1 128 + 1 6 - 1 8

2 π K 5 - 8 + 3 + 64 - 48 384 = 2 π K 5 11 384

11 π K 960

Ufa! Terminou! Então o momento de inércia em torno do eixo z é 11 π K 960 .

Resposta

a ) 0,0 , 7 12

b ) 11 π K 960

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule o momento de inércia de um sólido homogêneo com a forma de um cone circular reto de altura h e o raio da base R , em relação a um eixo passando pelo vértice e perpendicular ao eixo do cone.
Calcule o momento de inércia do cubo homogêncio de aresta L , em relação a um eixo que contém uma das arestas.
Calcule o momento de inércia de uma esfera homogênea de raio R , em relação a um eixo cuja distância ao centro seja h
Calcule o momento de inércia do corpo homogêneo x + y + z ≤ 4 , x ≥ 0 , y ≥ 0 e z ≥ 0 , em relação ao eixo z .
Calcule o momento de inércia de um cone circular reto de altura h , raio da base R , homogêneo, em relação a um diâmetro de sua base.