Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 15.8 - Ex. 36

Calcule a integral, transformando para coordenadas esféricas

∫ 0 3 ∫ 0 9 - y 2 ∫ x 2 + y 2 18 - x 2 - y 2 x 2 + y 2 + z 2 d z d x d y

Passo 1

E aí, gente boa! Firmeza?

A questão pede que a gente calcule:

∫ 0 3 ∫ 0 9 - y 2 ∫ x 2 + y 2 18 - x 2 - y 2 x 2 + y 2 + z 2 d z d x d y

Transformando em coordenadas esféricas. A mudança para o sistema de coordenadas esféricas é realizada fazendo a seguinte substituição:

{ x = ρ ϕ   c o s c o s   θ     y = ρ ϕ   θ     z = ρ c o s c o s   ϕ    

E:

d V = ρ 2 ϕ   d ρ d ϕ d θ

Também usamos a equação:

ρ 2 = x 2 + y 2 + z 2

Então, o que precisamos fazer aqui é transformar nossa função do integrando e nossos limites de integração em coordenadas esféricas. Para isso, vamos precisar entender qual região nossos limites em coordenadas retangulares estão descrevendo, pra gente tentar descrever a mesma região em coordenadas esféricas.

Vamos lá!

Passo 2

Começamos escrevendo nossa função em coordenadas esféricas:

f x , y , z =   x 2 + y 2 + z 2

Substituindo:

ρ 2 = x 2 + y 2 + z 2

Ficamos com:

f x , y , z = ρ 2

Ficamos com:

∭ E ρ 2   d V

Como:

d V = ρ 2 ϕ   d ρ d ϕ d θ

Ficamos com:

∭ E ρ 2 ϕ   d ρ d ϕ d θ

Passo 3

Note que ainda não temos nossos limites de integração que é dado por esse nosso sólido E. Precisamos entender quem ele é para podermos escrever os limites de integração após a mudança do sistema de coordenadas.

O nosso sólido está limitado abaixo pelo cone

z = x 2 + y 2

e acima pela superfície esférica

z = 18 - x 2 - y 2

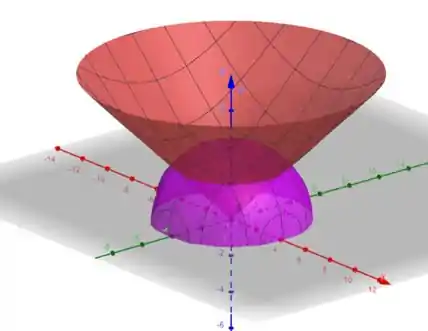
Interseção cone e esfera

Além disto, a projeção desse sólido no plano x y nos dá o primeiro quadrante de uma circunferência de raio 3 (sendo esta obtida através da interseção do cone com a esfera).

No final, o nosso sólido corresponde a 1/4 de um sorvete! Pois é, a nossa figura bem que parece com um sorvete!

Por causa dessa geometria, os limites de integração são:

0 ≤ ρ ≤ 18

0 ≤ θ ≤ π 2

0 ≤ ϕ ≤ π 4

Observem que o valor de ρ variou de 0 até 18 para poder descrever todos os pontos acima do cone e abaixo da superfície esférica. O valor de ϕ foi de 0 (eixo z ) até π / 4   pois este valor é a inclinação do nosso cone. Já o valor de θ é devido a projeção estar apenas no primeiro quadrante do plano x y . Sendo assim, a integral que precisamos resolver é:

∫ 0 3 ∫ 0 9 - y 2 ∫ x 2 + y 2 18 - x 2 - y 2 x 2 + y 2 + z 2 d z d x d y

Transformando para as coordenadas cilíndricas:

= ∫ 0 π / 4 ∫ 0 π / 2 ∫ 0 18 ρ 2 ⋅ ρ 2 ϕ   d ρ d θ d ϕ

Perceba que apareceu mais um termo no integrando. Isto se dá pelo Jacobiano da transformação!

Passo 4

Agora, só nos falta resolvermos a nossa integral! Vamos as contas então!

∫ 0 π / 4 ∫ 0 π / 2 ∫ 0 18 ρ 2 ⋅ ρ 2 ϕ   d ρ d θ d ϕ

∫ 0 π / 4 ∫ 0 π / 2 ϕ   ⋅ ρ 5 5 0 18 d θ d ϕ = ∫ 0 π / 4 ∫ 0 π / 2 ϕ   ⋅ 324 ⋅ 18 5 d θ d ϕ

∫ 0 π / 4 ϕ   ⋅ 324 ⋅ 18 5 ⋅ θ 0 π 2 d ϕ = ∫ 0 π / 4 ϕ   ⋅ 162 ⋅ 18 π 5 d ϕ

162 ⋅ 18 π 5 ⋅ - c o s c o s   ϕ   0 π 4 = 162 ⋅ 18 π 5 ⋅ - 2 2 + 1 = 81 18 π ⋅ 2 - 2 5

81 18 π ⋅ 2 - 2 5 = 486 π 2 - 1 5

Resposta

∫ 0 3 ∫ 0 9 - y 2 ∫ x 2 + y 2 18 - x 2 - y 2 x 2 + y 2 + z 2 d z d x d y = 486 π 2 - 1 5

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcular ∭_T^() ( x^2 + y^2 + z^2 ) . d V , onde T é a esfera x^2 + y^2 + z^2 = 9 e exterior ao cone z^2 = x^2 + y^2
Calcular ∭_T^() ( x ) . d V , onde T é a região limitada por x^2 + ( y - 3 )^2 + ( z - 3 )^2 = 9 .
Calcular as seguintes integrais:int_(- 1)^1 int_0^(sqrt(1 - x^2)) int_0^(sqrt(1 - x^2 - y^2)) ( e^(x^2 + y^2 + z^2) ) d z . d y . d x
Calcular ∭_T^() ( sqrt(x^2 + y^2 + z^2) ) d V , onde T é a região delimitada por x^2 + y^2 + z^2 = 1 e x^2 + y^2 + z^2 = 4 .
Calcular ∭_T^() ( x^2 + y^2 ) d V , onde T é o sólido delimitado por 4 = x^2 + y^2 + z^2 = 9 .