Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 11.12 - Ex. 17
- Aproxime por um polinômio de Taylor com grau em .
- Use a desigualdade de Taylor para estimar a precisão da aproximação quando estiver no intervalo dado.
- Verifique seu resultado na parte b) plotando
Passo 1
Fala, meu povo! Tudo certo?
Temos que fazer três coisas nesta questão: determinar o polinômio de Taylor; estimar a precisão da aproximação no intervalo dado; plotar e verificar o resultado da aproximação. Tudo isso para a função:
Com os dados:
Primeiro, um polinômio de Taylor em com grau tem o seguinte formato:
Para aproximar nossa função para um polinômio basta a gente substituir nos termos acima, os valores das derivadas primeira, segunda e terceira de .
Para achar a precisão da aproximação entre o polinômio de Taylor que vamos achar e a função no intervalo de , podemos usar a desigualdade de Taylor:
Nessa equação, é o erro entre o valor da função e do polinômio de Taylor. Para encontrar , usamos a desigualdade:
Onde é o valor máximo da derivada de de ordem . Já os termos e foram dados no enunciado, lembra? Então nossa tarefa aqui é encontrar o valor de que podemos usar na inequação e assim podemos achar o valor do erro .
Para verificar o resultado da letra , podemos plotar as curvas e , já que a diferença entre as duas é a definição do resto (ou erro):
Dito tudo isso, mão na massa!
Passo 2
Sendo assim, precisamos começar escrevendo o polinômio de Taylor. Como a questão nos disse que e , o nosso polinômio será:
Portanto, temos que determinar as derivadas parciais e aplicar no ponto . Desta forma,
Portanto, o polinômio de Taylor é:
Passo 3
A desigualdade de Taylor nos diz que
Onde . Portanto, para descobrirmos quem é , precisaremos descobrir primeiro quem é , e depois aplicar , pois esse é seu ponto de máximo dentro do intervalo que o enunciado deu.
Sendo assim, a quarta derivada da função é:
Calculando: :
Portanto, podemos tomar como . Como , o erro será máximo quando . Desta forma, temos:
Calculando a expressão, temos finalmente que:
Passo 4
Para compararmos o erro, vamos utilizar softwares para plotar a curva . Portanto, temos:
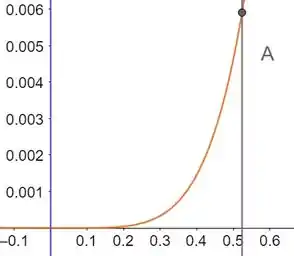
Esse ponto A é onde temos . Para esse valor temos , que representa o erro, menor que . E com isto, verificamos que o erro calculado foi menor que o erro real!
Resposta
- O resultado real é realmente menor que o erro calculado.
