Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 15.6 - Ex. 15
Calcule a integral tripla.
Em que é um sólido tetraédrico com vértices = e
Passo 1
Vamos lá meu amigo, nesse exercício, iremos analisar a seguinte integral:
Sob a região T que é o tetraedro com vértices e .
A imagem a seguir ilustra a região de interesse descrita no enunciado:
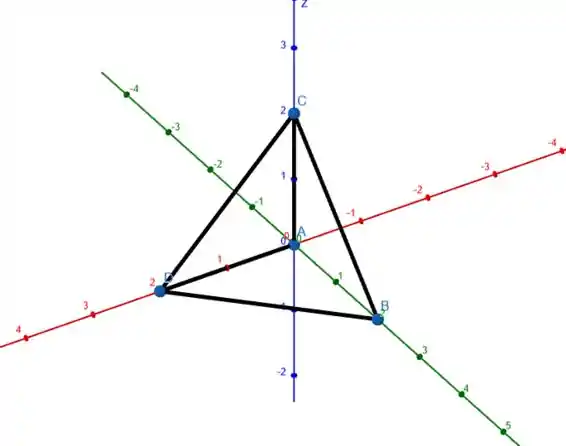
Temos que pensar uma forma de escrever essa integral com os limites de integração de modo que possamos realizar a integral interada de “dentro pra fora”, após isso é “só” calcular a integral.
Passo 2
Vamos analisar nossos limites de integração:
Veja, os vértices do tetraedro são: e
Veja que varia de até da seguinte forma:
Sendo que varia segundo:
Enquanto podemos dizer que varia de .
Dessa forma, podemos reescrever a integral como:
Veja que poderíamos ter feito de qualquer outra forma, desde que os pontos estivessem corretos. Isso afetaria também a ordem de integração. Pois sempre a integral que possui apenas “constantes” no limite de integração é a mais “externa”
Passo 3
Iremos calcular a integral como uma integral iterada, dessa forma, começando por :
Iremos fazer a integral “mais interna primeiro”
Simplificando:
Voltando à integral:
Passo 4
Agora podemos calcular a integral em função de :
“Isolando” a integral de “dentro”:
Veja que podemos considerar como constante
Substituindo os valores:
E, simplificando, obtemos:
Passo 5
E por fim, podemos resolver a integral em função de :
Por substituição:
Então temos:
Simplificando e aplicando os limites de integração:
E, dessa forma o valor da integral é: