Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 15.6 - Ex. 17
Calcule a integral tripla.
Passo 1
Nesse exercício, iremos analisar a seguinte integral:
Sob a região E que é delimitada pelo parabolóide e o plano .
A imagem a seguir ilustra a região de interesse descrita no enunciado:
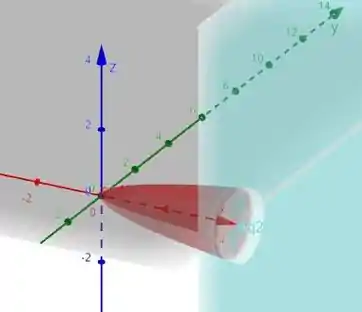
Dessa forma, com base na imagem, podemos reescrever a integral como:
Note que não especificamos um intervalo de integração para e ainda, não se preocupe, faremos isso na sequência, pois iremos mudar o sistema de coordenadas para o sistema polar, uma vez que a projeção da superfície E sobre o plano possui o formato de um disco. Iremos calcular a integral como uma integral iterada, dessa forma, começando por :
Se substituírmos a equação do plano na equação do parabolóide, obtemos:
Que é a equação de um círculo ao redor da origem com raio 1.
Passo 2
Agora, conforme visto no passo 1, iremos mudar o sistema de coordenadas para o sistema polar, para isso, faremos , dessa forma, temos:
E, utilizando a relação fundamental , obtemos:
E, simplificando, obtemos:
Passo 3
Agora podemos separar as integrais em e :
Resolvendo as integrais simultaneamente, obtemos:
E, dessa forma o valor da integral é: