Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 15.6 - Ex. 16

Calcule a integral tripla.

∭ T x z   d V , onde T é o tetraedro sólido com vértices ( 0,0 , 0 ) , ( 1,0 , 1 ) , ( 0,1 , 1 ) e ( 0,0 , 1 )

Passo 1

Fala, galerinha! Tudo certinho?

A questão quer a integral:

∭ T x z   d V

Onde T é um tetraedro com vértices 0,0 , 0 ,   1,0 , 1 ,   0,1 , 1 e ( 0,0 , 1 ) .

Uma integral tripla em relação a V é uma integral que está buscando o volume de um sólido:

V T = ∭ T d V

Bom, então falta o que falta para calcularmos essa integral tripla são os limites de integração para cada variável, x , y e z .

Então nosso objetivo nessa questão é olharmos o sólido tridimensional e sua projeção no plano x y para entendermos qual o limite de integração de cada variável.

Com os limites de integração em mãos, é só arranjarmos a integral na ordem que acharmos mais prático e calcular nossa integral iterada, começando da integral de dentro até a integral mais externa.

Vamos lá!

Passo 2

Vamos começar entendendo como é definida a região T para cada variável. As imagens a seguir ilustram a região de interesse descrita no enunciado:

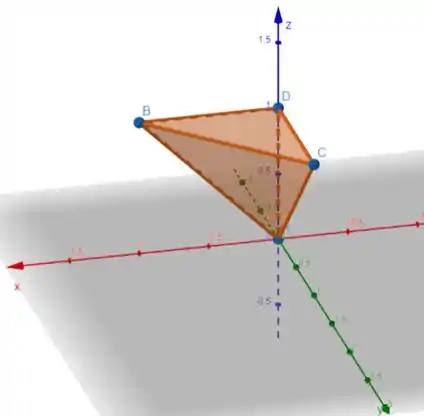
Tetraedro tridimensional

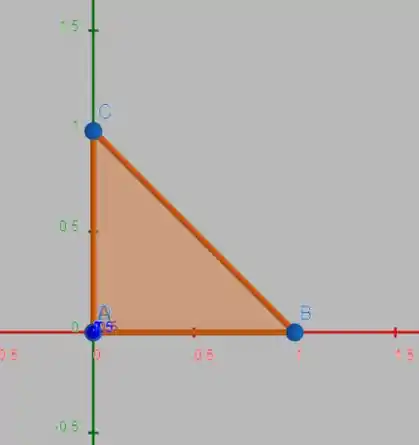
Projeção no plano x y

Vamos achar os intervalos para cada variável:

  • x : pela imagem da projeção do tetraedro, vemos que os valores no eixo x variam de 0 até 1:

    • 0 ≤ x ≤ 1

  • y : olhando novamente pela imagem tridimensional, vemos que y varia de 0 até o plano que liga os pontos B e C . Essa reta pode ser escrita como:

    • y = z - x

    Então:

    0 ≤ y ≤ z - x

  • z : Olhando a imagem tridimensional, vemos que z vai da reta z = x até o plano z = 1

x ≤ z ≤ 1

Dessa forma, com base nas imagens, podemos reescrever a integral como:

∫ 0 1 ∫ x 1 ∫ 0 z - x x z d y d z d x

Uma dica é sempre deixarmos as integrais que tem variáveis nos limites de integração “pra dentro” da integral.

Passo 3

∫ 0 1 ∫ x 1 ∫ 0 z - x x z d y d z d x

Iremos calcular a integral como uma integral iterada, dessa forma, começando por y , que é a integral de dentro. Aqui as outras variáveis são consideradas constantes:

∫ 0 1 ∫ x 1 x z y y = 0 y = z - x d z d x

Aplicando os limites de integração:

= ∫ 0 1 ∫ x 1 x z z - x - 0 d z d x

Simplificando a expressão, temos:

∫ 0 1 ∫ x 1 x z 2 - x 2 z d z d x

Passo 4

∫ 0 1 ∫ x 1 x z 2 - x 2 z d z d x

Agora podemos calcular a integral em função de z . Aqui x será considerada constante.

∫ 0 1 1 3 x z 3 - 1 2 x 2 z 2 z = x z = 1 d x

Aplicando os limites de integração:

= ∫ 0 1 1 3 x 1 3 - 1 2 x 2 1 2 - 1 3 x x 3 - 1 2 x 2 x 2   d x

E, simplificando, obtemos:

∫ 0 1 1 3 x - 1 2 x 2 - 1 3 x 4 + 1 2 x 4   d x

Passo 5

∫ 0 1 1 3 x - 1 2 x 2 - 1 3 x 4 + 1 2 x 4   d x

E por fim, podemos resolver a integral em função de x :

1 6 x 2 - 1 6 x 3 + 1 30 x 5 0 1 = 1 6 1 2 - 1 6 1 3 + 1 30 1 5 - 0

= 1 6 - 1 6 + 1 30 - 0

E, dessa forma o valor da integral é:

∭ x z   d V = 1 30

Resposta

∭ x z   d V = 1 30

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule a integral tripla. ∭ E sen ⁡ y d V Onde, E está abaixo do plano z = x e acima da região triangular com vértices 0,0 , 0 , π , 0,0 e 0 , π , 0 .
Calcule a integral tripla.
Calcule a integral tripla. ∭ E sen ⁡ y d V Onde E está abaixo do plano z = x e acima da região triangular com vértices 0,0 , 0 , π , 0,0 e 0 , π , 0 .
Esboce o sólido cujo volume é dado pela integral iterada. ∫ 0 1 ∫ 0 1 - x ∫ 0 2 - 2 z d y d z d x