Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 15.7 - Ex. 15
Calcule a integral tripla
Onde é limitado pelo parabolóide e pelo plano
Passo 1
Opa, tudo certinho?
Esse exercício pede pra gente calcular a integral tripla:
é delimitado pelo pelo parabolóide e pelo plano
Uma integral tripla em relação a é uma integral que está buscando o volume de um sólido:
Acima da região e abaixo da superfície de uma função.
Bom, então falta o que falta para calcularmos essa integral tripla são os limites de integração para cada variável, , e .
Então nosso objetivo nessa questão é olharmos o sólido tridimensional e sua projeção no plano , que é a região , para entendermos qual o limite de integração de cada variável.
Com os limites de integração em mãos, é só arranjarmos a integral na ordem que acharmos mais prático e calcular nossa integral iterada, começando da integral de dentro até a integral mais externa.
Bora lá!
Passo 2
Bom, então vamos lá! Vamos entender que limites são esses:
Nessa questão aqui, o parabolóide não tá escrito de forma usual. Geralmente a gente tem a equação do tipo , só que agora a nossa equação é . Desse jeito não vai ser tão diferente do que a gente tá acostumado, mas tem que prestar atenção pra não dar mole, beleza?
Lembra que geralmente nós temos o sólido com o eixo no eixo e a região de integração no plano ? Agora teremos o sólido com o eixo coincidindo com o eixo e a região de integração no plano .
Como o nosso parabolóide é paralelo ao eixo vamos usar o sistema de coordenadas cilindricas definido da seguinte forma:
Show ? É como se tivessemos feito uma rotação de eixos! É basicamente o que costumamos fazer, mas dessa vez vamos deixar nosso paraboloide em função de ao invés de , já que o eixo do paraboloide coincide com o eixo .
E o jacobiano é aquele mesmo de coordenadas cilindricas, então
Beleza! A nossa integral então vai ficar
Passo 3
Agora temos que determinar os limites de integração! Só pra guiar a gente, aqui um esboço do parabolóide e do plano
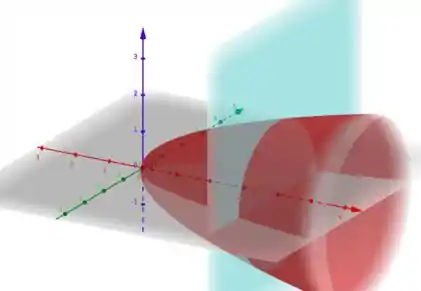
Paraboloide e Plano
Do desenho, podemos ver que varia do paraboloide
(em vermelho)
até o plano
(em azul)
então já temos que:
Para passar esse nosso intervalo para coordenadas cilincindricas usamos as seguintes equações:
Então,
- Intervalo para :
- Intervalo para :
- Intervalo para :
Substituindo, temos:
Colocando em evidência e usando o fato de que:
Ficamos com:
Então:
Pegando o valor máximo de e aplicando na equação do parabolóide:
Dividindo toda a equação por 4:
Substituindo novamente por
E usando a propriedade:
Podemos escrever:
Isolando :
Então vamos ter:
Pela nossa figura também temos que
Show! Agora é só montar a integral!
Passo 4
A nossa integral fica assim:
Colocamos por dentro a integral que tem variáveis nos limites de integração.
Começamos a integração por dentro, com a integral em relação a , tratando como constante:
Aplicando os limites de integração:
Simplificando:
Integrando em relação a :
Aplicando os limites:
Finalizando com a integral de :
Aplicando esses limites:
Show! O resultado da nossa integral será
Show! Conseguimos :D