Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 15.3 - Ex. 45
Calcule a integral trocando a ordem de integração.
45.
Passo 1
Fala, galera!
A questão quer que a gente resolva a integral invertendo a ordem de integração, ou seja, em vez de resolver , iremos resolver . Show, né?
Mas atenção! Se invertemos isso, precisaremos também inverter os limites de integração. Belê?
O primeiro passo é esboçar a região com as informações que temos dessa integral do enunciado.
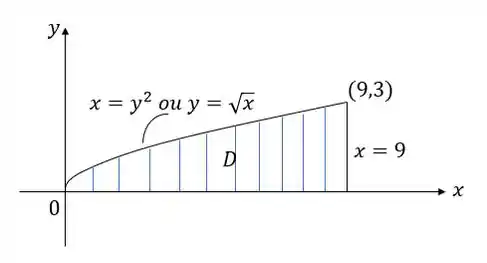
Ou seja, nessa região , os nossos limites de integração são:
Agora, invertendo a ordem, ficarão assim:
Passo 2
No final das contas, teremos
Então, basta calcular de dentro para fora, primeiro em relação a :
Substituindo, vamos fazer a mágica acontecer!
Cancelando a raiz com o expoente quadrado,
Agora integrando em relação a :
Colocamos a fração para fora da integral, como se fosse uma constante
Pela técnica da substituição, vamos chamar
Assim,
Cancelando os termos e colocando a fração para fora também:
Resolvendo a integral, ficaremos com:
Como sabemos quem é :
E substituindo os limites de integração, vamos fazer tudo ficar top!