Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 15.3 - Ex. 53

Calcule a integral trocando a ordem de integração.

∫ 0 1 ∫ a r c s e n   y π / 2 cos ⁡ x   1 + cos 2 ⁡ x   d x   d y

Passo 1

O primeiro passo é esboçar a região de integração: enquanto y varia no intervalo [ 0,1 ] , x vai da curva x = a r c s e n   y (ou y = s e n   x ) até a reta x = π / 2 .

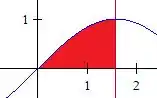
Mudando a ordem de integração, temos que y vai do eixo x até a curva y = s e n   x , com x no intervalo 0 , π / 2 :

∫ 0 1 ∫ a r c s e n   y π / 2 cos ⁡ x   1 + cos 2 ⁡ x   d x   d y = ∫ 0 π 2 ∫ 0 s e n   x cos ⁡ x 1 + cos 2 ⁡ x   d y   d x

Passo 2

Fazendo a primeira integral em y :

∫ 0 π 2 ∫ 0 s e n   x cos ⁡ x 1 + cos 2 ⁡ x   d y   d x = ∫ 0 π 2 s e n   x cos ⁡ x   1 + cos 2 ⁡ x   d x

Note que se chamarmos u = 1 + cos 2 ⁡ x , temos que d u = - 2 cos ⁡ x   s e n   x   d x . Assim,

∫ 0 π 2 s e n   x cos ⁡ x   1 + cos 2 ⁡ x   d x = - 1 2 ∫ 2 1 u   d u = 1 2 ∫ 1 2 u   d u = 1 3 u 3 1 2

Portanto,

∫ 0 1 ∫ a r c s e n   y π / 2 cos ⁡ x   1 + cos 2 ⁡ x   d x   d y = 1 3 ( 2 2 - 1 )

Resposta

1 3 ( 2 2 - 1 )

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Inverta a ordem de integração.
Inverta a ordem de integração.
Inverta a ordem de integração.
Inverta a ordem de integração.
Inverta a ordem de integração.