Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 8.1 - Ex. 15

Calcule a integral int x^3 . e^x d x usando integração por partes

Passo 1

O enunciado pede que para resolvermos essa integral utilizemos a integração por partes, para isso é preciso lembrar a fórmula:

int u d v = u . v - int v d u

No entanto, caso haja repetições de integração por partes utilizamos uma maneira mais organizada e que facilita os cálculos, que é a integração tabular.

Passo 2

Separamos int x^3 . e^x d x em f(x) = x^3 e g(x) = e^x ,e seguida montamos a tabela:

f(X) e suas derivadas g(x) e suas integrais

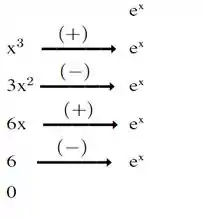
Passo 3

Depois multiplicamos as funções ligadas e combinamos elas de acordo com os sinais das operações indicadas.

int x^3 . e^x d x = x^3 . e^x - 3 x^2 . e^x + 6 x . e^x - 6 . e^x

= e^(x ) ( x^3 - 3 x^2 + 6 x - 6 ) + c

OBS: acrescentamos ao final o C (constante de integração)

Resposta

int x^3 . e^x d x = e^(x ) ( x^3 - 3 x^2 + 6 x - 6 ) + c

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Utilize o item (a) do exercício 3, calcule:a ) int sen^3 x d x
Utilize o item (a) do exercício 3, calcule:b ) int sen^4 x d x
Verifique que para todo natural n ≥ 1 e todo real s0 . ∫ t n e - s t d t = - 1 s t n e - s t + n s ∫ t n - 1 e - s t d t
Verifique que, para todo natural n != 0 , tem-se:b ) int cos^n x d x = (1)/(n) cos^(n - 1) x sin x + (n - 1)/(n) int cos^(n - 2) x d x
Verifique que, para todo natural n ≠ 0 , tem-se: a ) ∫ sen n ⁡ x d x = - 1 n sen n - 1 ⁡ x cos ⁡ x + n - 1 n ∫ sen n - 2 ⁡ x d x