Enunciado
Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 2.3 - Ex. 21
Calcule o limite, se existir.
21)
Passo 1
Fala aí, pessoal. Tudo belezinha?
Bom, essa questão é bem direta. Ela pede pra gente calcular o limite da função
Quando tende a . Ou seja
Para isso, a primeira coisa que temos que fazer é substituir o por na função e ver se é possível terminar o cálculo do limite. Se, por acaso, cairmos em alguma indeterminação matemática, teremos que modificar um pouco a função para conseguir calcular.
Vem comigo que te ajudo com isso no passo a passo.
Passo 2
Começamos calculando o limite com:
Opa! Caímos mesmo em uma indeterminação do tipo . Vamos tentar modificar um pouco essa função então para tentar recalcular.
Passo 3
Uma ferramenta que ajuda muito a gente são os produtos notáveis. Um deles é a diferença de quadrados, do tipo:
Podemos adaptar um pouquinho nossa função, fazendo:
Que pode ser escrito como:
E olha como isso vai facilitar nossa vida. Com isso nosso limite pode ser escrito como:
E simplificando, teremos:
Agora basta recalcularmos o limite.
Passo 4
Para calcular esse limite vamos usar a propriedade 2:
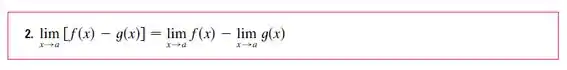
Além disso, vamos usar a propriedade de número 11:
Usando a de número 7 e 8:
E prontinho. Limite calculado.