Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 11.2 - Ex. 6
Calcule pelo menos dez somas parciais da série. Faça o gráfico de ambas as sequências de termos e de somas parciais na mesma tela. Parece que a série é convergente ou divergente? Se ela for convergente, calcule a soma. Se for divergente, explique por quê.
Passo 1
Beleza, galera?
Vamos começar calculando as 10 primeiras somas parciais da sequência:
No formato com até .
Depois mostraremos o gráfico tanto de (termos da sequência) quanto de (termos da série) n e vamos analisar o comportamento desses pontos e o que ele nos indica sobre a convergência ou divergência da nossa série, ou seja, se ela se aproxima de algum valor específico conforme seus termos crescem.
Por fim vamos precisar achar nossa soma de fato. Nossa vantagem aqui é que aqui temos uma série geométrica que é do tipo:
Onde é a razão da série.
Esse tipo de série converge se .
Por fim, esse tipo de série tem expressão pronta para cálculo da soma, facilitando bastante nosso processo de resolução:
Vamos passo a passo!
Passo 2
Bora calcular as primeiras dez somas parciais da série?
Lembrando que a soma parcial é dada por:
onde
Para :
Para :
Para :
Para :
Chegando na metade! Para :
Para :
Para :
Para :
Para :
Finalizando, para :
Passo 3
Show! Agora vamos fazer o gráfico da sequência de termos e o gráfico da sequência de somas parciais :
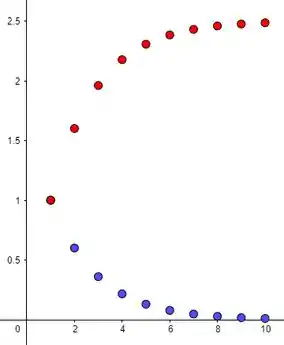
Em azul, a sequência de termos; em vermelho, a sequência de somas parciais
Olhando pro gráfico da sequência de termos, ele parece convergir pra , que seria uma condição necessária (mas não suficiente) pra série convergir.
E se a gente olhar pro gráfico da sequência de somas parciais, ele parece convergir pra algo em torno de , será?
Passo 4
Pra confirmar nossa observação do gráfico, vamos calcular a soma da série. Manipulando um pouco os termos podemos reescrever nossa série como:
Olha só, isso é a soma infinita de uma progressão geométrica com razão .
Como a nossa série converge e vai ter uma soma, que podemos calcular por:
O primeiro termo é , então:
Exatamente como pensamos, né mesmo?
Resposta
Série convergente