Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 8.3 - Ex. 34

Calcule os momentos M x e M y e o centro de massa de uma lâmina com a densidade e o formato dados

Passo 1

Fala, galera! Beleza? Vamos resolver essa questão!

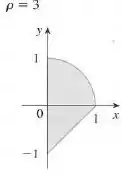
O enunciado pediu pra gente calcular o momento do sistema e seu centro de massa com base no gráfico da função dada e sabendo que a densidade é ρ = 3 .

Para isso, vamos usar as definições dos momentos M x e M y :

M x = ρ ∫ a b 1 2 f x 2 d x

M y = ρ ∫ a b x f ( x ) d x

E calcularemos as coordenadas do centro de massa C m = x - ,   y - , dadas por:

x - = M y m

y - = M x m

Então, vamos encontrar a nossa função e substituir os valores que o enunciado nos deu nas equações dos momentos. Depois, vamos usar os valores dos momentos para calcular as coordenadas do centro de massa.

Vamos lá!

Passo 2

Vamos observar o gráfico que ele nos deu:

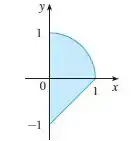
Repare que temos 1 4 de um círculo e uma reta formando a nossa figura.

O quarto de círculo possui a seguinte equação:

y = 1 - x 2

E a reta, observando os pontos do gráfico, nos dá a seguinte equação:

y = x - 1

Podemos então escrever as integrais, substituindo essas funções, na forma:

M x = ρ ∫ 0 1 1 2 1 - x 2 2 - x - 1 2 d x

M y = ρ ∫ 0 1 x 1 - x 2 - x - 1 d x

Passo 3

Resolvendo as integrais, temos:

M x = 3 2 - 2 3 x 3 + x 2 0 1

M x = 1 2

E

M y = 3 - 1 3 1 - x 2 3 2 - 1 3 x 3 + 1 2 x 2 0 1

M y = 3 2

Substituindo esses valores nas coordenadas do centroide, temos:

x - = M y m = 3 2 3 4 π + 2

x - = 2 π + 2

E

y - = M x m = 1 2 3 4 π + 2

y - = 2 3 π + 2

Então, o nosso centro de massa se encontra no ponto C 2 π + 2 ,   2 3 π + 2 .

Prontinho, galera! Até a próxima! 😉

Resposta

M x = 1 2

M y = 3 2

x - ,   y - = 2 π + 2 ,   2 3 π + 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma empresa estima que a receita marginal (em dólares por unidade) realizada pela venda de x unidades de um produto é 48 -0,0012 x . Supondo que a estimativa seja precisa, encontre o aumento na receit
Uma mineradora estima que o custo marginal de extração de x toneladas de cobre de uma mina é 0,6 +0,008 x , medido em milhares de dólares por tonelada. Os custos iniciais são $ 100.000 . Qual é o cust
Um cinema cobra $10,00 por pessoa e está vendendo aproximadamente 500 ingressos em uma noite típica de semana. Depois de pesquisar seus clientes, o cinema estima que, para cada 50 centavos de desconto
Calcule a integral indefinida ∫ x 3 + x x 4 + 2 x 2 7 d x
Calcule a integral indefinida ∫ s 2 s + 3 d s