Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 8.3 - Ex. 35

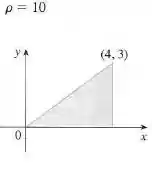
Calcule os momentos M x e M y e o centro de massa de uma lâmina com a densidade e o formato dados

Passo 1

Bom galera, nesse exercício iremos encontrar os momentos M x e M y e o centro de massa de uma lâmina. Para isso iremos utilizar os conceitos de centro de massa e momento.

Passo 2

A reta possui a seguinte equação

y = 3 4 x

Podemos então escrever a seguintes integrais

M x = ρ ∫ 0 4 1 2 3 4 x 2 d x

M y = ρ ∫ 0 4 x 3 4 x d x

Passo 3

Resolvendo as integrais, temos

M x = 45 16 x 3 3 0 1 = 60

M y = 15 2 x 3 3 0 1 = 160

Podemos encontrar o centroide utilizando a seguinte relação

x - = M y m = 160 60 = 8 3

y - = M x m = 60 60 = 1

Resposta

M x = 60

M y = 160

x - ,   y - = 8 3 ,   1

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Verifique por derivação que a fórmula está correta. ∫ tan 2 ⁡ x d x = tan ⁡ x - x + C
Encontre a integral indefinida geral. ∫ 5 + 2 3 x 2 + 3 4 x 3 d x
Encontre a integral indefinida geral. ∫ 2 + tan 2 ⁡ θ d θ
Encontre a integral indefinida geral. ∫ 2 t 1 + 5 t d t
Encontre a integral indefinida geral. ∫ 1 + r r 2 d r