Enunciado
Cálculo - Um curso de Cálculo Volume 2 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 4.1 - Ex. 3e
Calcule:
Onde
Passo 1
Primeiramente, vamos tentar visualizar essa função no plano, para podermos dividir a integral em algumas integrais.
A função é , então ela vai ser uma função constante entre e . Para o restante dos valores a função é , vamos esboçar esse gráfico então
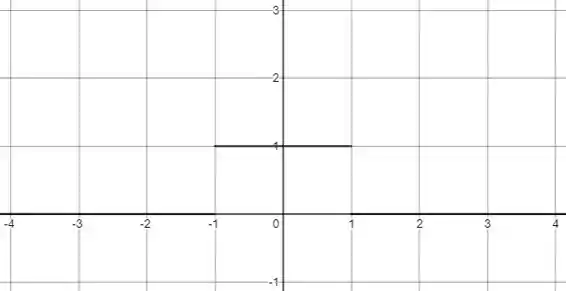
Para os intervalos e a função vale e não existe área debaixo do gráfico, portanto podemos resumir a integral em
Passo 2
E essa integral é elementar
Resposta
Exercícios de Livros Relacionados
Use o Teorema da Comparação para determinar se a integral é convergente ou divergente: ∫ 1 ∞cos 2 x 1 + x 2
Use o Teorema da Comparação para determinar se a integral é convergente ou divergente: ∫ 1 ∞d x x + e 2 x
Use o Teorema da Comparação para determinar se a integral é convergente ou divergente: ∫ 1 ∞x 1 + x 6 d x
Determine se a integral é convergente ou divergente. Calcule aquelas que são convergentes.
Determine se a integral é convergente ou divergente. Calcule aquelas que são convergentes.