Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diomara - Cálculo Diferencial e Integral de Funções de Várias Variáveis- Ed: 3º - Capítulo 7.12 - Ex. 7

Sejam F x , y , z = ( x , y , z ) um campo vetorial em R 3 e W a pirâmide de vértices O ,   A ,   B ,   C , onde O = 0,0 , 0 , A = 0,1 , 0 , B = 0,0 , 1 , C = c , 1,0   ( c > 0 ) . Calcule o valor de c sabendo que

∬ S W F     .   n d S + ∬ S A B C ( F     .     n ) d S = 1 ,

onde S W é a superfície da pirâmide W , S A B C é a face de vértices A ,   B ,   C , e n é o campo de vetores normais apontando para fora da pirâmide.

Passo 1

Se liga! O enunciado está pedindo para encontrar o fluxo. Para começarmos a resolver, podemos escrever que o fluxo, que chamaremos de ϕ , é dado por

ϕ = ∬ S W F     .   n d S + ∬ S A B C ( F     .     n ) d S = 1 .

Passo 2

Como o enunciado nos forneceu a localização dos vértices da pirâmide

O = 0,0 , 0

A = 0,1 , 0

B = 0,0 , 1

C = c , 1,0   ( c > 0 )

podemos então fazer um esboço da figura para entendermos melhor as áreas desejadas.

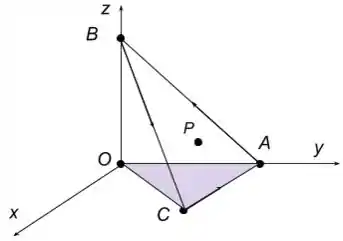
Usando a geometria podemos identificar que o lado O C -

y = x c ⇒ x = y c .

Vamos chamar a região pintada, que corresponde a base da pirâmide, de região D .

Passo 3

Agora podemos definir a equação para o plano A B C .

B P - = x - 0 , y - 0 ,   z - 1 = x , y , z - 1 B C - = c - 0 ,   1 - 0 ,   0 - 1 = c ,   1 , - 1         B A - = 0 - 0 ,   1 - 0 ,   0 - 1 = 0 ,   1 , - 1        

Podemos montar uma matriz com os valores acima e calcular o determinante, sabendo que ele é ZERO, pois as retas são coplanares, para achar a relação entre z e y .

x y z - 1 c 1 - 1 0 1 - 1 = - x + c z - 1 - c y + x = 0

z = 1 - y

Passo 4

Considerando que temos uma superfície fechada, podemos aplicar o Teorema de Gauss.

∬ S F →     .   n →   d s = ∭ W d i v F → d V     ( 1 )

Onde

d i v   F → = ∂ F 1 ∂ x + ∂ F 2 ∂ y + ∂ F 3 ∂ z .

Fazendo as derivadas parciais, temos

∂ F 1 ∂ x = ∂ ∂ x x = 1

∂ F 2 ∂ y = ∂ ∂ y y = 1

∂ F 3 ∂ z = ∂ ∂ z z = 1

⇒ d i v   F → = 1 + 1 + 1 = 3         ( 2 )

Portanto

∭ W d i v F → d V = ∬ D ∫ 0 P l a n o A B C 3   d z     d x d y   3 .

Passo 5

Agora nosso trabalho é resolver esta a integral acima. Para isso precisamos definir os intervalos de integração.

0 ≤ z ≤ 1 - y

0 ≤ x ≤ c y

0 ≤ y ≤ 1

Portanto a equação (3) fica

∭ W d i v F → d V = ∫ 0 1 ∫ 0 c y ∫ 0 1 - y 3   d z   d x   d y

= ∫ 0 1 ∫ 0 c y   3 1 - y d x   d y = ∫ 0 1 3 1 - y c y   d y

= ∫ 0 1 3 c ( y - y 2 )   d y = 3 c y 2 2 - y 3 3 0 1 = c 2

Assim podemos escrever que

∬ S W F     .   n d S = c 2

Passo 6

Agora precisamos olhar para

∬ S A B C ( F     .     n ) d S

Podemos escrever que

∬ S A B C ( F     .     n ) d S = ∬ D ( F ϕ x , y   n ( x , y )   ) d x d y

Começaremos fazendo a parametrização do plano A B C .

Como temos um campo de vetores apontando para fora da pirâmide, podemos escrever o campo exterior como

n x , y = ( 0,1 , 1 )

E

ϕ x , y = x , y , 1 - y ∈   D .

Reescrevendo a integral acima, teremos

∬ D x , y , 1 - y   .     0,1 , 1 d x d y = ∬ D y + 1 - y   d x d y

= ∬ D d x d y

O resultado da integral acima tem como resultado a área da região D . Sabendo que a região corresponde a um triângulo de base c e altura 1 , temos que

∬ D d x d y = c 2

Logo

∬ S A B C ( F     .     n ) d S = c 2

Passo 7

Como foi dito no enunciado

∬ S W F     .   n d S + ∬ S A B C ( F     .     n ) d S = 1

Podemos substituir as integrais pelos seus respectivos resultados

c 2 + c 2 = 1

Então podemos concluir que

c = 1 .

Resposta

c = 1 .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O que é mais razoável esperar: d i vF → = 0o ud i vF → ≠ 0 ?
Considere um escoamento no aberto Ω de R 3 , com velocidade v → = ( x , y , z ) , cujas componentes são supostamente de classe C1 em Ω. Suponha que derive de um potencial (isto é, que existe φ: Ω → ℝ,
Calcule o laplaciano da função φ dada. φ x , y = x y φ x , y = ln ⁡ x 2 + y 2 φ x , y = a r c t g x y ,y0 φ x , y = 1 4 e x 2 - y 2
Considere um fluido em escoamento com velocidade v → x , y , z = yj → , y0 .O fluido é incompressível? Por quê?Determine ρ , que só dependa de y , que satisfaça a equação de continuidade.Suponha que a
Sejam u → , v → : Ω ⊂ R 3 → R 3 dois campos vetoriais e φ : Ω → R um campo escalar. Em cada caso, faça hipóteses adequadas sobre φ ,u → ,v → e prove. (suponha u → = P i → + Q j → + R k →ev → = P 1 i →