Enunciado
Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 11.7 - Ex. 5
Calcule .
Passo 1
Aqui vamos usar essa propriedade da integral, se é uma função ímpar e contínua no intervalo , então:
Temos que uma função é denominada ímpar quando para todo do domínio de , e podemos ver isso quando observamos uma simetria.
Passo 2
Vemos abaixo pelo gráfico de que ele é ímpar:
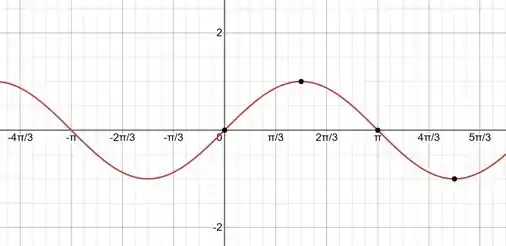
E pelo gráfico de é uma função par:
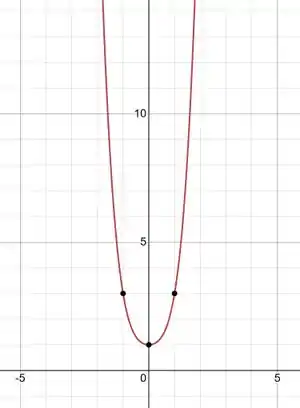
Assim temos que a nossa função na integral é uma função ímpar. Como o intervalo é simétrico podemos logo dizer que
Resposta
Exercícios de Livros Relacionados
Efetue a antidiferenciação. ∫ 3 + s s + 1 2
Use a fórmula de substituição do Teorema 7 para calcular as integrais nos Exercícios 1-46. ∫ 0 π 3 cos 2 x sin x d x ∫ 2 π 3 π 3 cos 2 x sin x d x
Use a fórmula de substituição do Teorema 7 para calcular as integrais nos Exercícios 1-46. ∫ 0 7 t t 2 + 1 1 / 3 d t ∫ - 7 0 t t 2 + 1 1 / 3 d t
Use a fórmula de substituição do Teorema 7 para calcular as integrais nos Exercícios 1-46. ∫ 0 3 y + 1 d y ∫ - 1 0 y + 1 d y
Use a fórmula de substituição do Teorema 7 para calcular as integrais nos Exercícios 1-46. ∫ 0 π / 4 tan x sec 2 x d x ∫ - π / 4 0 tan x sec 2 x d x