Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo Numérico - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 5.10 - Ex. 1

Calcule o valor aproximado da integral definida dada pela regra do trapézio com o valor de n indicado. Expresse o resultado com três casas decimais. Ache o valor exato da integral definida e compare-o com a aproximação.

∫ 0 2 x 3 d x ;   n = 4

Passo 1

Para resolver essa questão nós vamos utilizar o seguinte teorema do método do trapézio: Se a função f for continua no intervalo fechado [ a , b ] e os números a = x 0 , x 1 , x 2 , … ,   x n = b formarem uma partição regular de [ a , b ] então:

∫ a b f x d x ≈ b - a 2 n [ f x 0 + 2 f x 1 + 2 f x 2 + … + 2 f x n - 1 + f ( x n ) ]

No nosso caso, a = 0 ,   b = 2 e n = 4 . Vamos efetuar a partição no intervalo [ 0,2 ] . Se n = 4 , então:

Δ x = b - a n = 2 - 0 4 = 1 2 = 0 , 5

Sendo assim, temos os valores abaixo para a partição feita em n = 4 subintervalos.

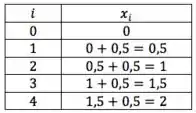
Passo 2

Agora vamos substituir todos os dados anteriores na fórmula:

∫ a b f x d x ≈ b - a 2 n [ f x 0 + 2 f x 1 + 2 f x 2 + 2 f x 3 + f ( x 4 ) ]

∫ 0 2 x 3 d x ≈ 2 - 0 2 ⋅ 4 [ f 0 + 2 f 0,5 + 2 f 1 + 2 f 1,5 + f ( 2 ) ]

∫ 0 2 x 3 d x ≈ 0,25 [ 0 + 2 0,5 3 + 2 1 3 + 2 1,5 3 + 2 3 ]

∫ 0 2 x 3 d x ≈ 0,25 0,25 + 2 + 6,75 + 8 = 0,25 17 = 4,25

∫ 0 2 x 3 d x ≈ 4,25 0

Sendo assim, o valor aproximado é 4,250 .

Passo 3

Para resolver a integral definida vamos utilizar a primitiva de um polinômio. Dessa forma,

∫ 0 2 x 3 d x = x 3 + 1 3 + 1 0 2 = 2 4 4 = 4

4 é o valor exato.

Podemos percebar uma diferença de 0,250 do valor exato e do aproximado.

Resposta

Valor aproximado 4,250 e exato é 4 .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Nos exercícios 105 e 106, use o segundo teorema fundamental do cálculo para calcular a integral definida. Então, encontre o valor de X que satisfaça o teorema do valor médio para integrais.105. ∫ 0 3
109. Se f x = x + x - 1 e F x = x , x1 x 2 - x + 1 , x ≥ 1 mostre que F é uma antiderivada de f em - ∞ , + ∞ .
103. Calcule ∫ 0 π cos ⁡ x + 1 2d x .
104. Formule um exemplo de uma função descontínua para a qual o teorema do valor médio para integrais (a) não se aplica e (b) se aplica.
107. Seja f contínua em [a,b] e ∫ a b f t ≠ 0 . Mostre que para qualquer k em (0,1) haverá um número c em (a,b) tal que ∫ a c f t d t = k∫ a b f t d t . ( Sugestão : considere a função F para a qual F