Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 15.Revisão - Ex. 9
Escreva como uma integral iterada, onde é a região mostrada e é uma função arbitrária contínua em .
Passo 1
Fala pessoal, tudo certo? Vamos entender nossa questão?
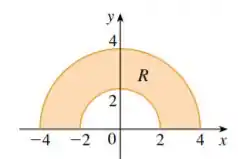
Ela pede pra gente descrever a integral como uma integral iterada onde é a região dada e uma função qualquer. Então, como só precisamos escrever a integral sem resolver. Precisamos identificar os limites em relação cada uma das coordenadas e escrever a integral. Veja que a figura tem um formato circular
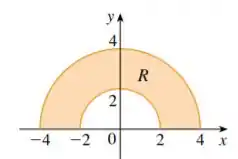
O que isso tem a ver conosco? Tem a ver que isso me diz que vale a pena utilizar coordenadas polares para facilitar.
Passo 2
Em coordenadas cartesianas essa região fica complicada de ser descrita, no entanto, se passarmos para coordenadas polares vamos ter o seguinte
Ou seja, nosso raio vai de 2 a 4 e a variação de ângulo vai de a para poder pegar exatamente a região sombreada. Uma coisa que não podemos esquecer ao passar para a forma polar é de multiplicar pelo jacobiano que é , dessa forma, nossa integral iterada vai ser escrita
da seguinte forma
Pronto, tá resolvido nosso problema. Falei que isso ser rápido?
