Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 15.Revisão - Ex. 17
Calcule o valor da integral múltipla.
Passo 1
E aí pessoal, tudo bom com vocês? Vamos lá!
Precisamos calcular a seguinte integral:
Onde é limitado por:
Para resolver, vamos primeiramente ter que achar os intervalos de integração. Ai sim montar nossa integral e resolvê-la.
Uma dica aqui, é vocês fazerem um esboço da região pois vai ficar muito claro os intervalos. Você vai perceber que temos uma região do Tipo I:
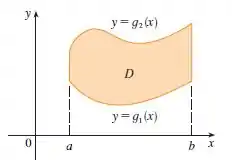
Ou pode observar os intervalos dados. Repare que já temos os intervalos de , certo?
Ele varia da curva que está abaixo até a curva que está acima . Logo, temos:
Para descobrir o intervalo de , vamos verificar quando na curva:
Vamos ter:
Logo, o intervalo de é:
Agora é só montar a integral e resolver.
Vamos nessa!!!
Passo 2
Vamos avaliar nossa região primeiro.
Onde é limitado por:
Fazendo o gráfico com o auxílio do Geogebra para uma melhor precisão, temos:
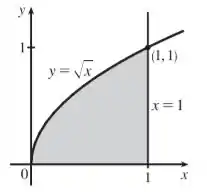
Observe que temos os intervalos exatamente como falamos no passo :
Isso é uma região do Tipo I.
Assim, conseguiremos reescrever nossa integral como sendo:
Passo 3
Beleza até aqui?!
Agora que temos nossa integral:
Podemos calcular seu valor de forma bem tranquila, integrando de dentro pra fora.
Então vamos começar integrando em , e tudo que não depender de y consideramos uma constante. Ficando assim:
Integrando em , temos:
Aplicando os limites de integração, tem-se:
Passo 4
Para resolver a integral em , vamos ter que fazer uma substituição do tipo:
Agora, ficamos com a seguinte integral simples a ser resolvida:
Integrando e voltando a variável , temos:
Aplicando os limites de integração, temos:
Como sabemos que
Temos como resposta: