Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 3.10 - Ex. 20
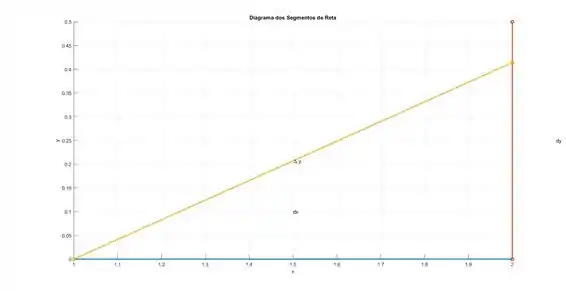
20) Calcule e para os valores dados de e . A seguir, esboce um diagrama como o da Figura 5, mostrando os segmentos de reta com comprimentos , e .
Passo 1
Oi meus lindoooos e lindaaaaaas, cêis tão baunzinhos??
Bora lá
O enunciado descreve uma situação em que temos uma função em termos de uma variável dada pela equação
A questão pede para calcular para valores específicos de
Aqui estão as definições dessas quantidades:
: Representa a mudança na variável dependente quando a variável independente é aumentada por uma quantidade
É calculado como a diferença entre os valores de \( y \) correspondentes a e
Representa a derivada da função com relação a multiplicada por Em outras palavras, é a taxa de variação instantânea de com relação a multiplicada pela mudança em
O enunciado fornece então estamos interessados em calcular para esses valores específicos.
Passo 2
A diferencial de uma função é dada por: :
Portanto, derivando a função:
Logo, a diferencial é:
Então temos:
E como então:
Passo 3
Temos a reta tangente em :
Logo, o gráfico é dado por:
