Calcule o volume do sólido obtido pela rotação do circulo em torno da reta

Bem, primeiramente vamos percerber que se fizermos uma rotação em uma esfera, ao redor do seu centro, ela sempre sera igual. Além disso, podemos percerber que a distância do centro da esfera até a reta é . Ou seja, girar a esfera ao redor da reta é análogo a girar, no eixo , uma esfera de mesmo raio, com origem em e . Portanto, vamos focar nessa esfera.

Para calcular esse solido de revolução, vamos ter que calcular a rotação da parte de cima da esfera, ou seja temos que girar o seguinte gráfico:

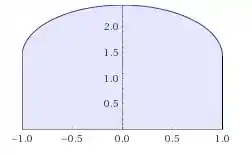
Porém, esse sólido não representa a esfera, para isso precisamos retirar a parte inferior, ou seja, temos que retirar a parte:

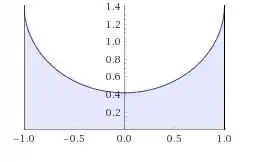
Dessa parte, a integral do volue se torna:

Bem, como , podemos fazer a seguinte substituição: