Enunciado
Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 13.9 - Ex. 6
Calcule o volume do sólido obtido pela rotação da região , em torno da reta .
Passo 1
Para resolver este problema, vamos usar o Teorema de Pappus para o volume. A gente vai usar essa fórmula aqui:
Onde:
O é a distância do centróide da figura até o eixo em torno do qual a figura gira.
A é a área da região que vai gerar o sólido, neste caso
Vamos olhar o gráfico gerado para poder identificar
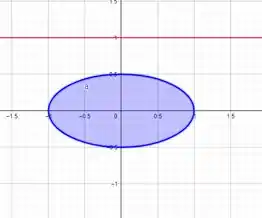
Como podemos ver, temos uma elipse de e a distância do centroide para o eixo
Passo 2
Agora é só aplicar na fórmula da área do círculo e substituir no teorema
Resposta
Exercícios de Livros Relacionados
Use o método de Newton (Seção 4.7), quando necessário, para aproximar as coordenadas x das intersercções das curvas com pelo menos quatro casas decimais; em seguida, use isso para aproximar a área da
Dois carros de corrida, lado a lado em uma pista reta, movem-se com funções velocidade v 1 t m / s e v 2 m / s , respectivamente. Suponha que ambos estejam alinhados no instante t = 60s . Interprete o
Encontre a região englobada pela curva y = s e nx e a reta que passa pelos pontos ( 0,0 ) e 5 π 6 , 1 2 na curva.
Encontre uma reta vertical x = k que divida a área englobada pelas curvas x = y , x = 2 e y = 0 em duas partes iguais.
Use o método de Newton (Seção 4.7), quando necessário, para aproximar as coordenadas x das intersercções das curvas com pelo menos quatro casas decimais; em seguida, use isso para aproximar a área da