Enunciado
Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 13.1 - Ex. 1m
Calcule o volume do sólido obtido pela rotação, em torno do eixo x, do conjunto de todos os pares (x,y), tais que :
Passo 1
Da para notar que essa questão tem um enunciado um pouco diferente, normalmente temos o isolado. Então faremos isso, isolaremos o :
Tirando as raízes quadradas, temos isso aqui ó:
Somando 2 de cada lado temos:
Agora nosso problema é fazer os volumes:
Passo 2
Com as funções já devidamente isoladas, daremos uma olhadinha nos gráficos, pois eles ajudarão a compreender o que está ocorrendo:
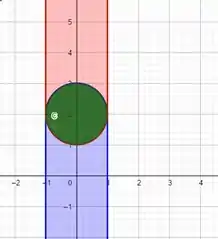
O gráfico em azul representa a região de volume :
O gráfico em vermelho representa a região de volume :
Em verde está a interseção, que é a região interna da circunferência da questão.
O Volume dessa figura rotacionada em torno do eixo , será dado por:
E os limites de integração serão de a .
Nesse passo, faremos a integral para acharmos a função. Vamos lá!
Faremos :
Quebrando a integral e tirando as constantes de dentro da integral, temos:
Faremos :
Quebrando a integral e tirando as constantes de dentro da integral, temos:
Passo 3
Nesse momento, teremos uma estratégia diferente das questões anteriores, antes fazíamos a integral de cada volume e depois subtraíamos, agora iremos subtrair antes, vamos sem medo:
Perceba que o primeiro e o último termo são iguais, então quando subtrairmos eles irão ficar igual a zero. Assim ó:
E o termo do meio será somado:
O nosso volume será dado por:
E agora finalmente, reduzimos nosso problema a uma integral definida, mas qual o método de integração ?
Integração por substituição trigonométrica, meu caro futuro engenheiro:
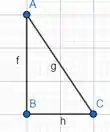
O cateto AB será dado pela função
O cateto BC será dado pela função
E a hipotenusa será dada pela função
Derivando, temos:
Substituindo tudo na integral da questão, temos:
Faremos agora a integral do problema que era: