Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 13.1 - Ex. 1j

Calcule o volume do sólido obtido pela rotação, em torno do eixo x, do conjunto de todos os pares (x,y), tais que :

1 ≤ x 2 + y 2 ≤ 4 e y ≥ 0

Passo 1

Vamos sempre começar com a nossa bússola que são os gráficos, vamos lá:

Inicialmente iremos fazer um esboço dos gráficos das figuras da questão:

1 ≤ x 2 + y 2 ≤ 4

y ≥ 0

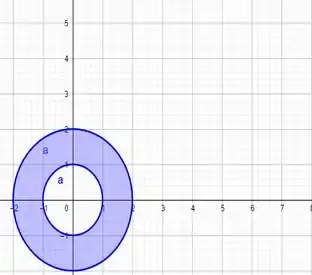
É apenas a região positiva de y, porém manteremos o costume de sempre fazer os gráficos, lembre-se nessas questões os gráficos são nossa bússola:

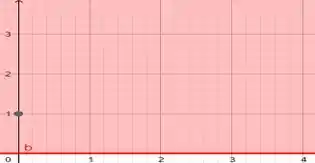
E agora a interseção entre esses dois gráficos, que estará representado de verde:

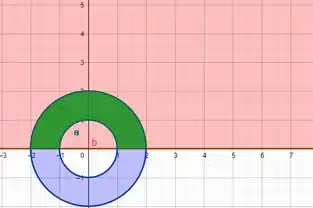
Passo 2

Retiraremos do último gráfico as nossas informações preciosas:

Primeiro perceberemos que essa figura é simétrica em relação ao eixo y, imagina que cortássemos a figura no eixo das ordenadas, não teríamos a mesma figura a esquerda e a direita?

Então ela é simétrica, mas isso ajuda no que? Poderemos fazer a integral a partir de 0 e depois multiplicarmos por 2.

Agora percebemos que o volume é dado pelo volume determinado pelos pontos x 2 + y 2 ≤ 4 com limite de integração de 0 a 2 e chamaremos esse volume de V 1

E o volume determinado por esses pontos x 2 + y 2 ≥ 1 com limite de integração de 0 a 1 e chamaremos esse volume de V 2 .

O Volume que procuramos é a diferença entre o V1 e o V2, lembrando que tenho que multiplicar por 2 por conta da simetria da figura:

Não esqueça a fórmula!

V = π ∫ y 2 d x

Passo 3

Vamos lá sem desanimo, toma sua água de engenheiro, cafezinho e respira, estamos no último passo:

Calcularemos V 1 ( y 2 = 4 - x 2 com limites de integração de 0 e 2):

π ∫ 0 2 4 - x 2 d x = π ∫ 0 2 4 d x - ∫ 0 2 x 2 d x = π 4 x 2 0 - x 3 3 2 0 = 16 π 3

Calcularemos V 2   ( y 2 = 1 - x 2 com limites de integração de 0 e 1):

π ∫ 0 1 1 - x 2 d x = π ∫ 0 1 d x - ∫ 0 1 x 2 d x = π   x 1 0 - x 3 3 1 0 = 2 π 3

Logo em sequência, daremos um xeque-mate na questão e lembramos que multiplicamos por 2 por conta da simetria hein, vamos lá:

V = 2 ( V 1 - V 2 ) = 2 16 3 π - 2 3 π = 28 3 π

Resposta

V = 28 3 π

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

53- Determinação do volume Determine o volume do sólido gerado pela rotação da região do primeiro quadrante delimitada pelos eixos coordenados, pela curva y = e x e pela reta x = ln ⁡ 2 em torno da re
54- Determinação de volume Determine o volume do sólido gerado pela rotação da região do primeiro quadrante delimitada pelos eixos coordenados, pela curva y = e x e pela reta x = 1 .Em torno da reta x
55- Determinação de volume Determine o volume do sólido gerado pela rotação da região do primeiro quadrante delimitada pelos eixos coordenados e pela curva y = cos ⁡ x ,0 ≤ x ≤ π / 2 , em tornoDo eixo
56- Determinação de volume Determine o volume do sólido gerado pela rotação da região delimitada pelo eixo das abcissas e pela curva y = x s e nx , 0 ≤ x ≤ π , em tornoDa reta x = π Veja o gráfico do
57- Considere a região delimitada pelos gráficos de y = ln ⁡ x , y = 0 e x = e .Determine a área da regiãoDetermine o volume do sólido formado pela rotação dessa região em torno do eixo das abscissas.