Enunciado
Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 13.1 - Ex. 1f
Calcule o volume do sólido obtido pela rotação, em torno do eixo x, do conjunto de todos os pares (x,y), tais que :
e
Passo 1
Nessa questão diferentemente das anteriores, teremos uma abordagem um pouco diferente! Mas por quê????
Pelo Simples fato de que não está limitado pela função , vamos ver como fica e tenho certeza que você terá entendido.
Faremos um gráfico para cada lado dessa inequação:. Como assim??
Assim ó: um gráfico de e outro de , facilitará muitooo a visualização!
Inicialmente iremos fazer um esboço dos gráficos da questão:
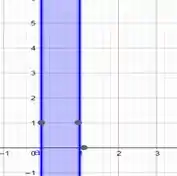
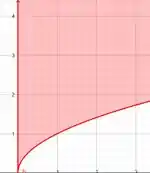
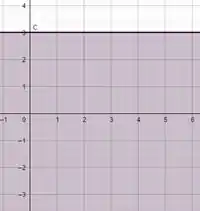
E agora a interseção de verde:
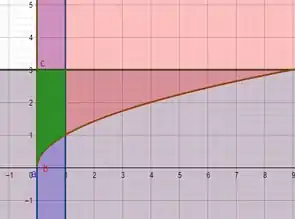
Passo 2
Extraindo coisas importantes do gráfico:
Primeiro o intervalo de integração, que será de
Pelo gráfico podemos perceber que o Volume da figura rotacionada será dada pela diferença entre o volume da figura rotacionada pelas regiões:
:
:
Passo 3
Nesse passo faremos a integral, como vimos no passo 2, teremos que fazer uma integral para cada volume() e depois diminuí-las:
(; :
(:
Finalmente, Ufaaaa, podemos calcular o volume pedido: