Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 13.1 - Ex. 1h

Calcule o volume do sólido obtido pela rotação, em torno do eixo x, do conjunto de todos os pares (x,y), tais que :

0 ≤ y ≤ x   e   x 2 + y 2 ≤ 2

Passo 1

Vamos ver essa questão. Os gráficos são relativamente conhecidos, porém em questões que envolva circunferência ou elipse, teremos que tomar muito cuidado com o sólido formado na rotação.

Inicialmente iremos fazer um esboço dos gráficos das figuras da questão:

  0 ≤ y ≤ x  

x 2 + y 2 ≤ 2

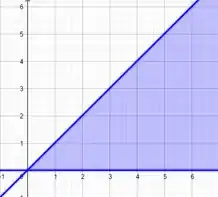
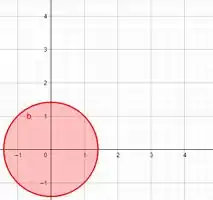
O interior de uma circunferência de raio √ 2 e centro ( 0,0 )

E agora a interseção entre esses dois gráficos de verde com as retas x = 1 e a x = 2 , essas retas ajudarão na hora de fazer a questão.

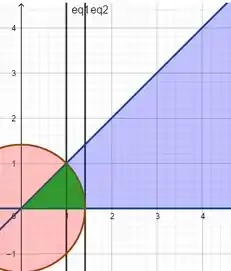
Passo 2

O que acontece nesse problema é que faremos o volume de 0 até 1 utilizando a reta y = x ,   chamaremos esse volume de V 1 .

Depois faremos o volume de 1 até 2 , utilizando a circunferência x 2 + y 2 = 2 , chamaremos esse volume de V 2 . O volume que queremos descobrir é a soma desses dois volumes:

Antes de fazermos o passo 3, deixarei aqui a fórmula do volume, caso você tenha estudado bastante hoje e tenha esquecido até seu nome:

V = π ∫ y 2 d x

Passo 3

Agora faremos cada volume, começaremos com V1

V1 ( y 2 = x 2 ) e lembrando que seus limites de integração são de 0 até 1

π ∫ 0 1 x 2 = π x 3 3 1 0 = π 3

V 2 ( y 2 = 2 - x 2 ) e lembrando que seus limites de integração são de 1 até 2 :

π ∫ 1 2 2 - x 2 d x = π ∫ 1 2 2 d x - ∫ 1 2 x 2 d x   =   π 2 x 2 1 - x 3 3 2 1 = π 4 2 3 - 5 3

Fazendo a soma final, nem parece que acabou né? Mentira, parece sim kkkkkk, ninguém estava aguentando mais!

V = V 1 + V 2 = π 3 + π 4 2 3 - 5 3 = 4 π 2 - 1 3

Resposta

V = 4 π 2 - 1 3

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

y = (2)/(x - 3)
17. Deduza a fórmula para o volume de uma esfera, rotacionando a região limitada pela circunferência x 2 + y 2 = r 2 e pelo eixo x em torno do eixo x .
26. Ache o volume do sólido gerado se a região do Exercício 24 girar em torno da reta y = 1 .
27. A região limitada pela curva y = c o t gx , pela reta x = π 6 , e pelo eixo x é girada em torno do eixo x . Ache o volume do sólido gerado.
18. Deduza a fórmula para o volume de um cone circular reto com h unidades de altura e a unidades de raio da base, rotacionando a região limitada pelo triângulo retângulo em torno de um de seus cateto