Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 13.1 - Ex. 1e

Calcule o volume do sólido obtido pela rotação, em torno do eixo x, do conjunto de todos os pares (x,y), tais que :

y ≥ 0 ,   1 ≤ x ≤ 2   e   x 2 - y 2 ≥ 1

Passo 1

A integração será um problema pequeno comparado a visualização, então preste bastante atenção nos gráficos, eles serão nossa bússola em problemas de volume de figuras rotacionadas.

Sem mais enrolação, vamos começar pelo que nos dará a direção, da uma olhadinha nesses gráficos que estão aqui em baixo:

Esse exercício requer 4 gráficos, vamos lá!

Inicialmente iremos fazer um esboço dos gráficos das figuras da questão:

x 2 - y 2 ≥ 1

Atenção: É a “parte de fora” dessa hipérbole:

y ≥ 0 :

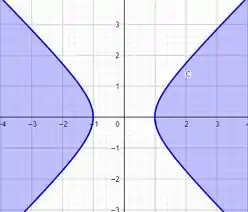
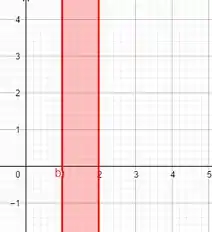
É apenas a região positiva de y, porém manteremos o costume de sempre fazer os gráficos, lembre-se nessas questões os gráficos são nossa bússola:

1 ≤ x ≤ 2 :

E agora a interseção entre esses dois gráficos em verde!

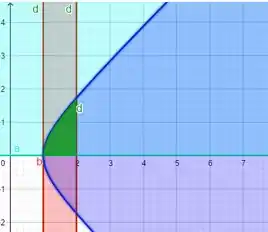
Passo 2

Faremos uma análise, apenas para notarmos as coisas úteis dos gráficos. O intervalo de integração, as retinhas que delimitam a figura de interseção dos gráficos, são x = 1   e   x = 2

Não se esqueça da fórmula!!!

V = π ∫ f ( x ) 2 d x  

Passo 3

Outra coisa importante em hipérboles é que queremos y 2 ou f 2 ( x ) para botar na nossa fórmula e a hipérbole, já nos dá isso. Como?????

Assim, ó:

x 2 - y 2 = 1

y 2 = x 2 - 1

Substituindo na nossa fórmula e lembrando que nosso intervalo de integração será de 1 a 2 temos isso aqui:

V = π ∫ 1 2 x 2 - 1   d x

Quebrando a nossa integral em duas:

V = π ∫ 1 2 x 2 d x - ∫ 1 2   d x = π x 3 3 2 1 - x 2 1 = 4 3 π

Resposta

V = 4 3 π

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

29. Ache o volume do sólido gerado pela rotação, em torno da reta x = - 4 , da região limitada por aquela reta e pela parábola x = 4 + 6 y - 2 y 2 .
30. Ache o volume do sólido gerado pela rotação, em torno do eixo x , da região limitada pela parábola y 2 = 4 x e pela reta y = x .
25. Ache o volume do sólido gerado se a região do Exercício 23 girar em torno da reta y = 1 .
31. Ache o volume do sólido gerado pela rotação, em torno da reta x = 4 , da região do Exercício 30.
33. Ache o volume do sólido gerado pela rotação, em torno da reta y = - 3 , da região limitada pelas parábolas y = x 2 e y = 1 + x - x 2 .