Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Um curso de Cálculo Volume 2 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 3.2 - Ex. 1h

Calcule o volume do sólido obtido pela rotação, em torno do eixo y, do conjunto de todos os (x, y) tais que

0 ≤ x ≤ 2 ,     y ≥ x - 1     e 0 ≤ y ≤ x 2

Passo 1

Primeiro precisamos entender o domínio desse conjunto.

Queremos os ponots (x,y) tais que obedeça a: 0 ≤ x ≤ 2 ,     y ≥ x - 1     e 0 ≤ y ≤ x 2 . Ou seja, queremos os pontos acima da linha que descreve a função     y = x - 1 e abaixo de y = x 2 , sendo também valores acima do eixo x. Os símbolos de ≥ e ≤ seimbolizam que os pontos definidos na função também fazem parte do conjunto. Ele também pede 0 ≤ x ≤ 2 porém y = x - 1 não é definido para x < 1 daí temos um novo intervalo:   1 ≤ x ≤ 2 .

Com isso, o gráfico fica mais ou menos assim:

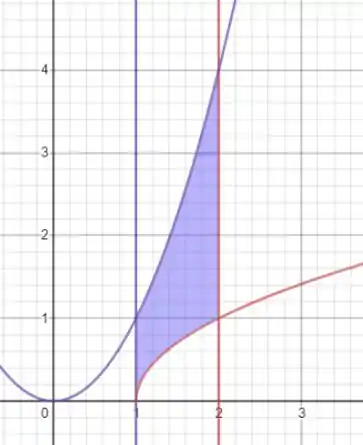
Essa será a área que vamos rotacionar em torno do eixo y.

Passo 2

Com esse gráfico em mãos vemos que se fizermos vários retângulos dentro dessa área com largura infinitesimal e altura variando entre as duas funções, podemos usar o método das cascas cilíndricas:

∫ a b 2 π r × h × d x

Sendo pro nosso caso o dx igual a largura infinitesimal, o r vai ser o ponto médio dessa largura(será x), e o f(x) vai ser a diferença entre as duas funções, ou seja, h = x 2 - x - 1 . Por fim, os nossos limites de integração são o intervalo de x, que como vimos é: 1 ≤ x ≤ 2 .

Reescrevendo, teremos:

∫ 1 2 2 π x × ( x 2 - x - 1 ) × d x

Agora, bora resolver isso aqui!

Passo 3

Primeiro fazemos a distributiva:

2 π ∫ 1 2 x 3 d x - ∫ 1 2 x x - 1 d x = 2 π x 4 4 2 1 - ∫ 1 2 x x - 1 d x

= 2 π 16 4 - 1 4 - ∫ 1 2 x x - 1 d x = 2 π 15 4 - ∫ 1 2 x x - 1 d x

Não sabemos resolver essa integral: ∫ 1 2 x x - 1 d x , mas sabemos resolver essa:   ∫ u u d u que é bem parecida.

Se tivéssemos um x - 1 antes da raíz em vez de só um x seria bem razoável usar a substituição u = x - 1 → d u = d x .

Podemos fazer isso! Vou mostrar como:

Concorda comigo que x = ( x + 0 ) ?

E que 0 = ( 1 - 1 ) ?

Então substituindo, ficamos com:

x = ( x + 1 - 1 )

Se agruparmos do jeito que podemos fazer a substituição, ficaremos com:

x = ( x - 1 + 1 )

Assim se substituirmos esse valor na integral, vamos ficar com:

= 2 π 15 4 - ∫ 1 2 x x - 1 d x = 2 π 15 4 - ∫ 1 2 ( x - 1 + 1 ) x - 1 d x =

Ótimo! Agora podemos resolver com u = x - 1 → d u = d x :

2 π 15 4 - ∫ 1 2 x - 1 + 1 x - 1 d x = 2 π 15 4 - ∫ 0 1 u + 1 u d u =

2 π 15 4 - ∫ 0 1 u u d u - ∫ 0 1 u d u = 2 π 15 4 - ∫ 0 1 u 3 2 d u - ∫ 0 1 u 1 2 d u

= 2 π 15 4 - 2 5 u 5 2 1 0 - 2 3 u 3 2 1 0 = 2 π 15 4 - 2 5 - 2 3 = 2 π 225 - 24 - 40 60 = 2 π 161 60

= 161 π 30

Resposta

V = ∫ 1 2 2 π x × ( x 2 - x - 1 ) × d x = 161 π 30

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Considere o sólido que resulta quando a região sombreada do Exercício 1 gira em torno da reta y = 2 . ( a ) Faça uma conjectura sobre qual é maior: o volume desse sólido ou o volume do sólido do Exerc
Determine se a afirmação dada é verdadeira ou falsa. Explique sua resposta. [Nestes exercícios, suponha que um sólido S de volume V seja delimitado por dois planos paralelos perpendiculares ao eixo x
Encontre o volume do sólido que resulta quando a região acima do eixo x e abaixo da elipse x 2 a 2 + y 2 b 2 = 1 ( a0 , b0 )
Suponha que v e w sejam funções contínuas em [ c , d ] e seja R a região delimitada pelas curvas x = v ( y ) e x = w ( y ) de y = c até y = d . Usando o método das arruelas, deduza e explique uma fórm
Encontre o volume do sólido que resulta quando a região delimitada pelas curvas dadas gira em torno do eixo y . x = csc ⁡ y ; y = π / 4 ; y = 3 π / 4 ; x = 0