Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 3.9 - Ex. 43

37) Uma câmera de televisão está posicionada a de uma base de lançamento de foguete. O ângulo de elevação da câmera deve variar a uma taxa que possa focalizar o foguete. O mecanismo de foco da câmera também deve levar em conta o aumento da distância entre a câmera e o foguete em subida. Vamos supor que o foguete suba verticalmente e com velocidade de quando já tiver subido .

(a) Quão rápido estará variando a distância da câmera ao foguete naquele momento?

(b) Se a câmera de televisão se mantiver sempre na direção do foguete, quão rápido estará variando o ângulo de elevação dela naquele mesmo momento?

Passo 1

Opa, bora lá! Imagina que a gente ta filmando o lançamento de um foguete! Posicionamos a câmara a da base de lançamento de foguete e a medida que o foguete sobe vamos aumentando esse ângulo pra focar.

O enunciado diz que quando o foguete esta em uma altitude de a sua velocidade vertical é de m/s. Sabendo disso temos que responder algumas coisas!

Item a: Quão rápido estará variando a distância da câmera ao foguete quando e a velocidade é m/s.

Vamos chamar de a distância entre a câmera e o foguete em metros, de a altura do foguete em metros e de o ângulo de inclinação em radianos.

Podemos encarar essa situação como um triângulo retângulo da seguinte forma:

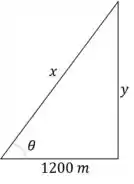
Logo, a relação entre e é:

Passo 2

Derivando em função do tempo em segundos, temos:

Logo, quando o foguete já tiver subido a uma taxa de variação , a taxa de variação da distância será dada por:

Portanto, a distância da câmera ao foguete varia a uma velocidade de .

Passo 3

Item b: Se a câmera de televisão se mantiver sempre na direção do foguete, quão rápido estará variando o ângulo de elevação dela naquele mesmo momento?

A relação entre a altura de foguete e o ângulo descrito é dada pela relação trigonométrica:

Passo 4

Agora, vamos derivar para correlacionar as taxas de variação:

Logo, quando o foguete já tiver subido a uma taxa de variação , a taxa de variação do ângulo é dada por:

Portanto, a taxa de variação do ângulo é .

Resposta

(a)A distância da câmera ao foguete varia a uma velocidade de .

(b)A taxa de variação do ângulo é .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O lucro de um varejista é $ 100 ⋅ y quando são gastos diariamente $ x em propaganda e y = 2500 + 36 x - 0,2 x 2 Use a derivada para determinar se seria lucrativo aumentar a verba de propaganda, consid

Se C(x) for o custo total da fabricação de x pesos de papel e C x = 200 + 50 x + x 2 5 Ache a função custo marginal;Ache o custo marginal quando x = 10.

Um balão mantém a forma de uma esfera enquanto está sendo inflado. Ache a taxa de variação da área da superfície com respeito ao raio no instante em que o raio for 2 m.

Duas partículas A e B movem – se para direita numa reta horizontal e partem de um ponto O. Seja s cm a distância orientada do ponto O em t s. As equações de movimento são s = 4 t 2 + 5 t (para a partí

Se R(x) for o rendimento total recebido das vendas de x aparelhos de televisão e R x = 600 x - 1 20 x 3 Ache a função rendimento marginal;Ache o rendimento marginal quando x = 20.