Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 16.5 - Ex. 10
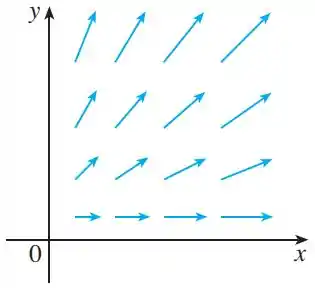
O campo vetorial é mostrado no plano e é o mesmo em todos os planos horizontais (em outras palavras é independente de e sua componente é ).
- O será positivo, negativo ou nulo? Explique.
- Determine se o . Se não, em que direção aponta?
Passo 1
Olá, tudo bem? Vamos analisar o que a questão quer.
Primeiro, ela diz que o campo vetorial no plano mostrado pela figura
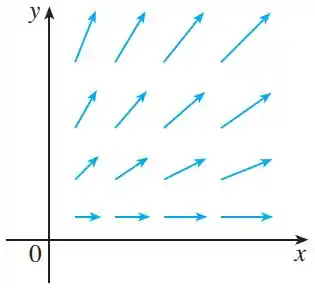
É o mesmo, caso a gente tente variar , ou seja, esse campo só existe nesse plano onde .
Lembrando que um campo vetorial qualquer em duas dimensões pode ser escrito assim:
Onde representa o eixo e representa o eixo .
O rotacional é esse aqui:
Onde representa o eixo
E o divergente é esse:
Tudo isso que mostrei é definido no livro, tá bom?
Na letra (a),
Ela quer a gente diga se o divergente desse campo é , negativo ou positivo e explicar o motivo.
Na letra (b),
A questão pede para dizer se o rotacional é , ou seja
Caso não seja, dizer para qual direção ele aponta.
Então, vamos primeiro analisar o campo vetorial e depois responderemos as perguntas, show?
Passo 2
Bora analisar esse campo!
Temos então que campo vetorial qualquer pode ser representado como
Para o gráfico dado
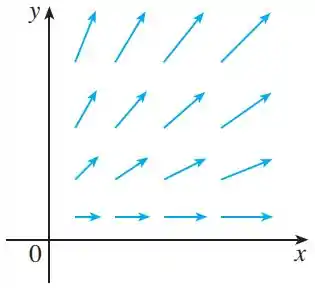
podemos perceber que a componente do campo , que é , aumenta à medida que aumenta (o vetor fica mais largo à medida que aumenta).
Então a variação em relação a é positiva
Mas não parece mudar à medida que aumenta então
Olhando para , que é a componente do campo vetorial, temos que a sua componente aumenta quando aumenta (o vetor vai ficando mais pra cima, quando aumenta).
Então sua variação é positiva
E não muda com a mudança de
Agora vamos para as letras!
Passo 3
- O divergente é calculado por
- Podemos calcular o rotacional por
Como
Temos que o só depende de valores positivos, logo o divergente é positivo.
Passo 4
Como
Substituindo os valores
Portanto temos que o rotacional é
Resposta
- Positivo