Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 16.5 - Ex. 9
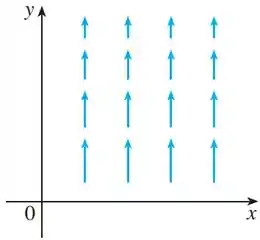
O campo vetorial é mostrado no plano e é o mesmo em todos os planos horizontais (em outras palavras é independente de e sua componente é ).
- O será positivo, negativo ou nulo? Explique.
- Determine se o . Se não, em que direção aponta?
Passo 1
Olá, tudo bem? Vamos analisar o que a questão quer.
Primeiro, ela diz que o campo vetorial no plano é mostrado pela figura:
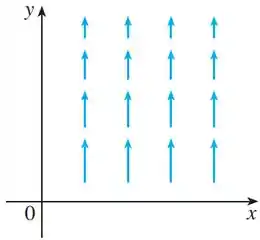
E esse campo é o mesmo, caso a gente tente variar , ou seja, esse campo é igual em qualquer plano paralelo ao plano .
Lembrando que um campo vetorial qualquer em duas dimensões pode ser escrito assim:
Onde representa o eixo e representa o eixo .
O rotacional é esse aqui:
Onde representa o eixo
E o divergente é esse:
Tudo isso que mostrei é definido no livro, tá bom?
Na letra (a), ela quer a gente diga se o divergente desse campo é , negativo ou positivo e explicar o motivo.
Na letra (b), a questão pede para dizer se o rotacional é , ou seja
Caso não seja, dizer para qual direção ele aponta.
Então, vamos primeiro analisar o campo vetorial e definir as derivadas parciais. Depois vamos aplicar nas fórmulas e responderemos as perguntas, talkei?
Passo 2
Bora analisar esse campo!
Temos então que um campo vetorial qualquer pode ser representado como
Para o gráfico dado
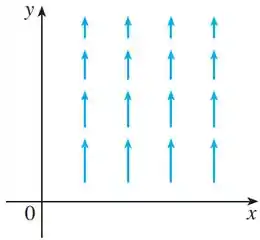
podemos perceber que a componente do eixo , que é , para todos os vetores do plano é igual a . Isso quer dizer que
porque nenhum desses vetores está virado para esquerda ou direita.
Agora, veja que os vetores também não mudam de direção enquanto se movem para cima. Se você subir ou descer, todos os vetores ainda estarão apontando para cima, exatamente da mesma maneira.
Isso significa que a variação em relação à é
E em relação à é também!
Portanto,
Olhando para a coordenada , temos que a sua componente no vetor , que é , diminui quando aumenta, portanto, sua variação é negativa
Pegue uma coluna qualquer e olhe para cima, verá que o vetor diminui de tamanho conforme aumenta.
E não muda com a mudança de e , ou seja, pegamos uma linha qualquer da figura e olhamos na direita e esquerda e notamos que o vetor continua o mesmo, portanto
Pronto, vamos para as letras!
Passo 3
- O divergente em duas coordenadas é calculado por
- o rotacional em duas variáveis se resume em
Como temos que
Como já analisamos e concluímos que
o divergente é negativo.
Passo 4
Como temos
Substituindo
Portanto temos que o rotacional é
Resposta
- Negativo