Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 6.1 - Ex. 47

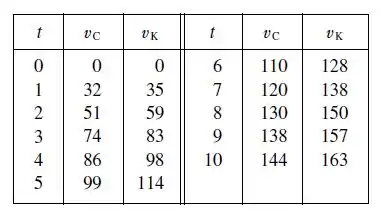
Os carros de corrida dirigidos por Chris e Kelly estão lado a lado na largada de uma corrida. A tabela mostra as velocidades de cada carro (em quilômetros por hora) durante os primeiros dez segundos da corrida. Use a Regra do Ponto Médio para estimar quão mais longe Kelly vai do que Chris durante os primeiros 10 segundos.

Passo 1

Muito bem galera, vamos ter que aplicar a Regra do ponto Médio. Bora relembrar?

∫ 0 10 v k - v c . d t = ∆ t [ v k - v c n = 1 + v k - v c n = 2 + v k - v c n = 3 v k - v c n = 4 + v k - v c n = 5 ]

Por que estamos usando v k - v c ?

Porque queremos estimar quão mais longe Kelly vai do que Chris durante os primeiros 10 segundos.

A variação da velocidade nós já temos, agora podemos decidir quantos intervalos vamos utilizar para estimar a resposta.

Vamos dividir em 5 intervalos, ou seja, n = 5 . Então ∆ t será calculado como:

∆ t = 10 s - 0 s 5 = 2 s

A velocidade está em km/h, então vamos relacionar:

∆ t = 2 s × 1 h 3600 s = 1 1800 h

Se nosso intervalo é de 2 em 2 segundos, portanto vamos usar t = 1 s ,     t = 3 s ,   t = 5 s ,   t = 7 s   e     t = 9 s , ou seja, os pontos intermediários:

= ∆ t . [ v k - v c t = 1 s + v k - v c t = 3 s + v k - v c t = 5 s v k - v c t = 7 s + v k - v c t = 9 s ]

Substituindo:

= 1 1800 h . [ 35 k m h - 32 k m h t = 1 s + 83 k m h - 74 k m h t = 3 s + 114 k m h - 99 k m h t = 5 s + 138 k m h - 120 k m h t = 7 s + 157 k m h - 138 k m h t = 9 s ]

= 1 1800 h . 3 k m h + 9 k m h + 15 k m h + 18 k m h + 19 k m h = 64 k m h

= 1 1800 h . 64 k m h = 0,036   k m

Em metros fica melhor, não é?

v k - v c = 0,036   k m × 1000   m 1 k m = 36   m

Resposta

v k - v c = 36   m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Nos Exercícios de 21 a 36, use o método desta secção para calcular a área da região dada; use retângulos inscritos ou circunscritos, conforme indicado. Para cada exercício, faça uma figuramostrando a
Nos Exercícios de 21 a 36, use o método desta secção para calcular a área da região dada; use retângulos inscritos ou circunscritos, conforme indicado. Para cada exercício, faça uma figuramostrando a
Nos Exercícios de 21 a 36, use o método desta secção para calcular a área da região dada; use retângulos inscritos ou circunscritos, conforme indicado. Para cada exercício, faça uma figuramostrando a
Nos Exercícios de 21 a 36, use o método desta secção para calcular a área da região dada; use retângulos inscritos ou circunscritos, conforme inficado. Para cada exercício, faça uma figura mostrando a
Nos Exercícios de 21 a 36, use o método desta secção para calcular a área da região dada; use retângulos inscritos ou circunscritos, conforme inficado. Para cada exercício, faça uma figura mostrando a